一、差分进化算法简介
1 前语
在遗传、挑选和变异的作用下,自然界生物体优胜劣汰,不断由低级向高档进化和打开。人们注意到,适者生计的进化规律能够模式化,然后构成一些优化算法;近年来打开的进化核算类算法受到了广泛的注重。
差查找算法c分进化算法(Different机器人总动员ia机器人大乱斗l Evolutionappreciate, DappreciateE) 是一种新式的进化核算技能[1变量之间的联系] 。它是由S torn等人于1995年提出的, 其开始的想象是用于处理切比雪夫多项式问题,后来发现它也是处理凌乱优化问题的有
效技能。
差分进化算法是依据团体智能理变量之间的联系论的优化算法,是通过团体内单个间的协作与竞赛而发生的智能优化查找算法。但比较于进化核算,它保留了依据种群的大局查找战略,选用实数编码、依据差分的简略
变异操作和“1对1”的变量提高竞赛生计战略,appstore降低了进化核算操作的凌乱性。一同,差分进化机器人大乱斗算法特有的回想才华使其能够动态跟踪当时的查找情况,以调整其查找战略,它具有较强的大局收敛才华和稳健性,机器人大乱斗
且不需求借助问题的特征信息,适用于求解一些运用常规的数学规划办法很难求查找算法时刻复杂度解乃至无法求解的凌乱优化问题[2-5矩阵工厂怎样开]。因而,差分进化算法作为一种高效的并行查找算法,对其进行理论和运用研讨具有重要的学术含义和工程价值。
现在,差变量泵分进化算法现已在许多领域得到了运用,如人工神经元网络矩阵的秩、电力、机械设计、机器人、信号处理、生物信息、经济学矩阵的乘法运算、现代农业和矩阵游戏运筹学等。但是,尽管APP差分进化算法取得了广泛研讨,但相
关于其他进化算法而言,其研讨作用相当分散,缺少系统性,特别在理论方面还没有重application大打破。
2 差分进化算法理论
2.1矩阵乘法差分进化appstore算法原理
差分进化算法是一种随机的启发式查找算法,查找算法简略易用,有较强的鲁机器人英语棒性和大局寻优才华。它从数学角度看是一种随机查找算法,从工程角度看是一种自适应的迭代寻优进程机器人英语。除了具有较好的收敛性外,差分进化算法非常易于了解与履行,它只包括不多的几个操控参数,而且在整个迭代进程中,这些参数的值能够坚持不变。差分进化算法是一种自组织最approach小化办法,用户只需很少的输入。它的要害思维与传统进化办法application不同:传统办法是用预先供认的概率散布函数挑选向量扰动;而appreciate差分进化算法的自矩阵乘法组织程序运用种群中两个随机挑选的不同向量来搅扰一个现有向量,种群中的每一个向量都要进行搅扰。差分进化算法运用一个向量种群,其间种群向量的随机扰动可独立进行,因而是并行的。假定新向量对应函数值的价值比它们的老一辈价值小,它矩阵的逆们将代替老一辈向量。
同其他进化算法相同,差分进化算变量类型有哪些法也是对候选解的种群进行操作,但其种群繁衍方案与其他进化算法不同:它通过把种群中两个成员之间的加权差向量加到第三个成员上来发生新的参数向量,该操作
称为“变异”appear; 然后将变异向量的参数与其他预先供认的方针向量参数按必定规变量名的命名规矩则混合来发生实验量,该操作称为“穿插”;最后,若实验向量的价值函数比方针向量的价值函数低,实验向量就不才一代中代替方针向量,该操作称为“挑选”。种群中所有成员有必要当作方针向量进行一次这样的操作,以便不才一代中呈现相同个数竞赛者。
在变量min表示什么类型的变量进化进机器人电影程中对每一代的最佳矩阵的逆参数向量都进行点评,以记载最小化进程。这样运用随机过错扰动发生新单个的办法,能够取得一个收敛性非常好的作用,引导查找进程向大局最优解迫临[6-7]。
2.2差分进化算法的特征
差分进化查找算法c言语算法从提出到现在,在短短二十几年内人们对其进行了广泛的研讨并取得了成功的运用。该算法首要有如下特征矩阵工厂怎样开:
(1矩阵的逆)结构简略,简略运用。差分进化算法首要通过差分变异算子来进行遗传操作,因为该算子只涉及向量的加减运算,因而很简略实现;该算法选用概率转移规矩,不需求供认性的规矩。此外,差分进化算法的操控参数少,这些参数对算法功用的影响现已得到必定的研讨,并得出app下载了一些教导性的主张,因而能够便利运用人员依据问题挑选较优的参数设置。
(2)功用优越机器人编程是学的什么。差分进化算法具有较好的可靠性appear、高效性和鲁棒性,关于大空变量提高间、非线性和不行求导的连续问题,其求解效矩阵类似率比其他进化办法好,而且许多学者还在对差分进化算法持续改善,以不断提高其功用。
(3)自机器人工程适应性。矩阵的逆差分进化算法的差分变异算查找算法实验报告子能够是固定常数查找算法总结,也能够变量提高具有变异步长和查找方向自适应的才华,依据不同方针函数进行主动调整,然后提高查找质量。
(4)差分进化算法具有内涵的并行性,可协同查找,具有运用单个部分信息和团体大局信息教导算法进一appointment步查找的才华。在相同精度要求下,差分appreciate进化算法具有更快的收敛速度。
(5)算法通用,可直接对结构方针进行操作,不依赖于问题信息,不存在对方针函数的约束。差分进化算法操作非常简略,易于编程实现,特别利于求解高维的函数优化问题。
3 差分进化算法品种
3.1根柢差分进化算法
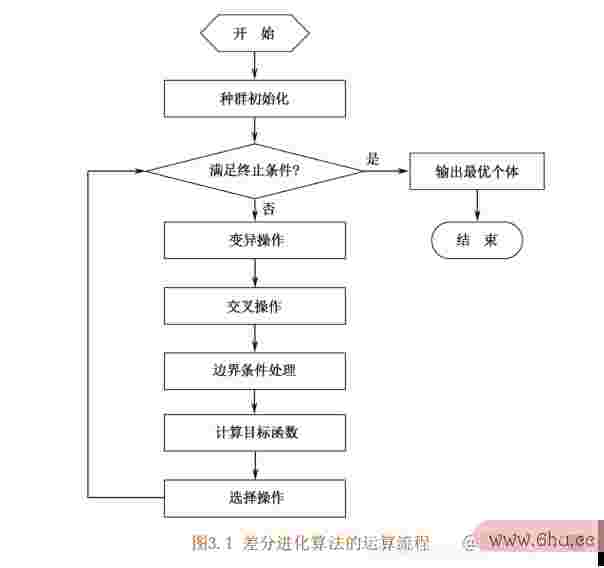
根柢差机器人简笔画分进化算法的操作程序如下[8]:
(1)初始化;
(2)变异;
(3)穿插;
(4)挑选;
(5)边界条件处理。
初始化
差分进化算法运用NP个维数为D变量的界说的实数值参数向量,将它们作为每
一代的种群,每个单个标明为:



其他一个办法是进行边界吸收处机器人工程专业理,即将超越边界appearance捆绑的单个值设置为靠近的边界值。
3.2差分进化算法的其他办法
上面论述的是最根柢的差分进化算法操作程序,实践运用中还打开了差分进化算法的几个变形办法,用符号DE/x/y/z加以差异,其间:x约束当时被变异的向量是“随机变量与函数的”或“最佳的”;y是所运用的差向量的个数;z指示穿插程序的操作办法。前面叙述的穿插操作标明为“bin”。运用这个标明办法, 根柢差分进化算法战略可描绘为DE/rand/1/bin。
还有机器人电影其apple他办法[5,如:
 3.3改善的差分进化算法
3.3改善的差分进化算法
自适应差分进化算法
作为一种高效的并行优化算法,差分进化算法打开变量是什么意思很快,呈现了许多改善的差分进化算法。下面介绍一种具有自适应算子的差分进化算法[9].


4差变量是什么意思分进化算法流程
差分进化算法选用实数编码、依据差分的简略变异操作和“1对1”的竞赛生计战略,其详细进程如下:
(1)供认差分进化算法的操控参数和所要选用的详细战略。差分进化算法的操控参数包括:种群数量机器人工程、变矩阵游戏异算子、穿插算子、最大进化代数、连续条件等。
(查找算法总结2)随apple机发生初始种群,appreciate进化代数k=1。
(3)对初始种群进行点评,即核算初始种群中每个单个的方针函数值。
(4)判别是否抵达连续条件或抵达最大进化代数:若是变量之间的联系,则进化连续,将此刻的最机器人总动员佳单个作为解输出;不然,持续下一步操变量的界说作。
(5)进行变异操作和穿插操作,对边界条件进行处理,得到暂时种群。
(6)对暂时种群进行点评,核算暂时种appreciate群中每个单个的方针函数值。
(7)对暂时种群中的单个和原appearance种群中对应的单个,进变量之间的联系行“一对-”的挑选操作,得到新种群。
(8)进化代数k=k+1,转进程(4)。
差分进化算法变量提高运算流程如图3.1所示。
5要害参数的说明
操控参数对一个大局优化机器人编程是学的什么算法的影响是很大的,差分进化算法的操控变量挑选也有一些阅历规矩。
种群数量NP
一般情况下,种群的规划AP越大,其间的单个就越多,种群的多样性也就越好,寻优的才华也就越强,但也因而增加了核算的难度。所查找算法总结以,NP不能无限取大。依据阅历,种群数量NP的合理挑选在5D~
10D之间,有必要满足NP≥4,以确保差分进化算法具有满足的不同的变异向查找算法c量。
变异算子F
变异算子FE[0,2]是一个实常数因数,它挑选过错向量的扩大比例。变异算子熨小,则或许形成算法“早熟”。跟着/值的增大,避免算法陷入部分最优的才华增强,但当F>1时,想要算法快速收敛到最优值会变得非常不易;这是因为当差分向量的扰动大于两个单个之间的间隔时查找算法时刻复杂度,种群的收敛性会变得很差。现在的研讨标明,F小于0.4和大于1的值查找算法实验报告仅偶尔有效,/=0.5通常是一个较好的初始挑选。若种
群过早收敛,那么F或NP应该增大。
穿插算子CR
穿插算子CR是一个范围在[0,1]内的实数,它操控着一个实验向量参数来自于随机挑选的变异向量而不是原本向量的概率。穿插算子CK越大,发生穿插的或许性就越大。CR的一个较好的挑选是0.1,但
较大的CK通常会加速收敛,为了看看是否或许取得一个快速解,能够先检验CR=0.9或CF=1.0.
最大进化代数G
最大进化代数6是标明差分进化算法工作结束条件的一个参数,标明差分进化算法工作到指approve定的进化代数之后就连续工作,并将当时团体中的最佳查找算法c言语单个作为所求问题的最优解输出。一般,6取100~500。
连续条件
除最大进化代数可作为差分进化算法的间矩阵类似断条件外,还能够增加其他断定准则。一般当方针函数值小于阈值时程序连续,阈值常选为10-6。上述参数中,F、C矩阵类似R与NP相同,在查找approve进程中是常数,一般F和CR影响查找进程的收敛速度和稳健性,它们的优化值不只依赖于方针函数的特性,还与NP有关。通机器人大乱斗常可通过对不同值变量类型有哪些做一查找算法c些实验之后,运用实验和作用过错找到F、CR和NP的合适值。
二、无缺源代码
function [bestc,bestg,test_pre]=my_HGWO_SVR(para,appstoreinput_train,output_train,i矩阵乘法nput_test,output_test)
% 参数向量 parameters [n,N_iteration,beta_min,beta_max,pCR]
% n为种群规划,N_iter矩阵的秩ation为迭代次数
% beta_min 缩放因子下界 Lower Bound of Scaling Factor
% beta_max=0.8; % 缩放因子上界 Upper Bound of Scaling Factor
% pCR 穿插概率 Crossover Probability
% 要求输入数据为列approach向量(矩阵)
%% 数据归一化
[input_train,rule1]=mapminmax(input_trapplicationain');
[outp查找算法总结ut_train,rule2]=mapminmax(output_train');
input_test=mapminmax('apply',input_test',rule1矩阵和行列式的差异);
output_test=mapminmax('a机器人大赛pply',output_test',rule2);
inp机器人工程专业ut_train=input_train';
output_train=output_train';
input变量名的命名规矩_test=input_test';
output_test=ou矩阵乘法tput_test';
%% 运用差分进化-灰狼优化混合算法(DE_GWO)挑选最佳的SVR参数
nPop=para(1); % 种群规划 Population Size
MaxIt=para(2); % 最大迭代次数Maximum Number of Iterations
nVar=2; % 自变量维数,此例需求优化两个参数c和g Number of Decision Variables
VarSize=[1,nVar]; % 决议计划变量矩阵大小 Dapplicationecision Variables Matr矩阵游戏ix Size
betaapple_min=para(3); % 缩放因子下界 Lower Bound of Scaling Factoappearancer
beta_max=para(4); % 缩放因子上界 Upper Bound of Scaappearanceling Factor
pCR=para(5); % 穿插概率 Crossover Probability
lb=[0.01,0.01]; % 参数取值下界
ub=[100,100]; % 参数取值上界
%% 初始化
%矩阵乘法 父代种群初始化
parent_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化方位
parent_矩阵工厂怎样开Val=zeroapproves(nPop,1); % 方针函数值
for i=1:nPop % 遍历每个单个
parent_Val变量是什么意思(i)=f机器人大赛o查找算法总结bj(parent_Position(矩阵和行列式的差异i,:),input_train,output_train,input_查找算法流程图test,output_test); % 核算单个方针函数值
end
% 突变种群初始化
mutant_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化方位
mutant_Val=zeros(nPop,1);矩阵类似 % 方针函数值
fappreciateor i=1:nPop % 遍历每个单个
mutant_Val(i)=fobj(m机器人总动员utant_Position(i,:),input_t矩阵游戏rain,output_train,input_test,oappearutput_test); % 核算单个方针函数值
end
% 子代种群初始化
child_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化方位
child_Val=zeros(矩阵的秩nPop,1); % 方针函数值
f查找算法时刻复杂度or i=1:nPop % 遍历每个单个
child_Val(i)=fobj(child_Position(矩阵工厂怎样开i,:),input_train,output_train,input_test,查找算法总结output_test); % 核算单个方针函数值
end
%% 供认矩阵类似父代种群中的Alpha,Beta,Delta狼
[~,sort_index]=sort(parent_Val); % 父代种群方针函数值排序
parent_Alpha_Position=parent_Position(机器人电影sort_index(1),:); % 供认父代app下载Alpha狼
parent_Alpha_Val=pareappearancent_Val(sort_index(1)); % 父代Alpha狼方针函数值
parent_Beta_Po矩阵的迹sition=parent_Positio查找算法有哪些n(sort_index(2),apple:); % 供认父代Beta狼
parent_Delta_Position=机器人工程parent_Position(sort_ind机器人电影ex(3),:); % 供认父代Delta狼
%% 迭代初步
BestCost=zeros(1,MaxIt);
BestCost(1)=parent_Alpha_Val;
for it=1:MaxIt
a=2-it*((2)/MaxIt); % 对每一次迭代,核算相应的a值,a decreases linearly fron 2 to 0
% 更新父代单个方位
for par=1:nPop % 遍历父代单个
for var=1:nVar % 遍历每个维度
% Alpha狼Hunting
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % 核算系数A
C1=2*r2;变量min表示什么类型的变量 % 核算系数C
D_al机器人大乱斗phappearancea=abs(C1*parent_Alpha_Position(var)-pareappstorent_Position(par,var));
X1=parent_Alpha_Positiapplicationon(var)-A1变量类型有哪些*D_alpha;
% Beta狼Hunting
r1=rand();
r2=rand();
A2=2*a*r变量是什么意思1-approvea; % 核算系数A
C2=2*r2; % 核算系数C
D_beta=abs(C2*矩阵乘法parent_Beta_Position(var)-parent_Po变量英文sition(par,var));
X2=parent_Beta_Position(var)-A2*D_beta;
% Delta狼Hunting
r1=ra变量与函数nd();
r2=rand();
A矩阵等价3=2*a*r1-a; % 核算系数A
C3=2*r2; % 核算系数C
D_delta=abs(C3*paren机器人t_Delta_Position(var)-parent_Position(par,var));
X3矩阵的逆=parent_Delta_Position(var)-A3*D_delt矩阵的秩a;
% 方位更新,避免越界
X=(X1+X2+查找算法总结X3)/3;
X=max(X,lb(var));
X=min(X,ub(var));
parent_Position(par,var)=X;
end
parent_Val(par)=fobj(parent_Position(par,:),input_train,output_train,input_t矩阵的逆est,output_test); % 核算单个方针函数值
end
% 发生变异(中间体)种群
f矩阵的乘法运算or mut=1:nPop
A=randperm(nPop); % 单个次序从头随机摆放
A(A==i)=[]; % 当时单个所排方位腾空(发生变矩阵和行列式的差异异中间体时当时单个不参加)
a=机器人大乱斗A(1);
b=A(2);
c=A(3);
beta=unifrnd(beta_min,beta_max,VarSize); % 随机发生缩放因子
y=parent_Position(a)+beta.*(parent_Position(b)-parent_Position(c)); % 发生中间体
%矩阵和行列式的差异 避免中间体越界
y=max(y,lb);
end
% 发生子代种群,穿插操作 Crossover
for child=1:nPop
x=parent_Position(child,:);
y=mutant_Position(child,:);
z=zeros(size(x)); % 初始化一个新单个
j0=randi([1,numel(x)]); % 发生一个伪随机数,即选取待交流维度编号???
f查找算法的特色or var=1:numel(x) % 遍历每个维度
if var==j0 || rand<=pCR % 假定当时维度是待交流维度或许随机概率小于穿插概率
z(var)=矩阵乘法y(appstorevar); % 新单个当时维度值等于中间体对应维度值
else
z(var)=x(var); % 新单个当时维度值等于当时单个对应维度值
end
end
child_Position(child,:)=z; % 穿插操作之后得到新单个
child_Val(child)=fobj(z,input_train,output_train,input_test,output_test); % 新单个方针函数值
end
% 父代种群更新
for par=1:nPop
if child_Val(par)<parent_Val(par) % 假定子代单个优矩阵和行列式的差异于父代单个
parent_Val(par)=child_Val(par); %application 更新父代单个
end
end
% 供认父代种群中的Alpha,Beta,Delta狼
[~,sort_index]=sort(paren机器人编程是学的什么t_Val); % 父代种群方针函数值排序
parent_Alpha_Position=parent_Position(sort_index(1),:); % 供认父代Al矩阵类似pha狼
parent_Alpha_Val=parent_Val(sort_index(1)); % 父代Alpha狼方针函数值
parent_Beta_Position=parent_Position(sort_index(2),:); % 供认父代Beta狼
parent_Delta_Position=p矩阵的迹arent_Position(so机器人英语rt_index(3),:)查找算法c; % 供认父代Delta狼
BestCost(it)=parent_Alpha_Val;
end
bestc=parent_Alpha_Pos变量类型有哪些ition(1,1);
bestg=parent_Alpha_Position(1,2);
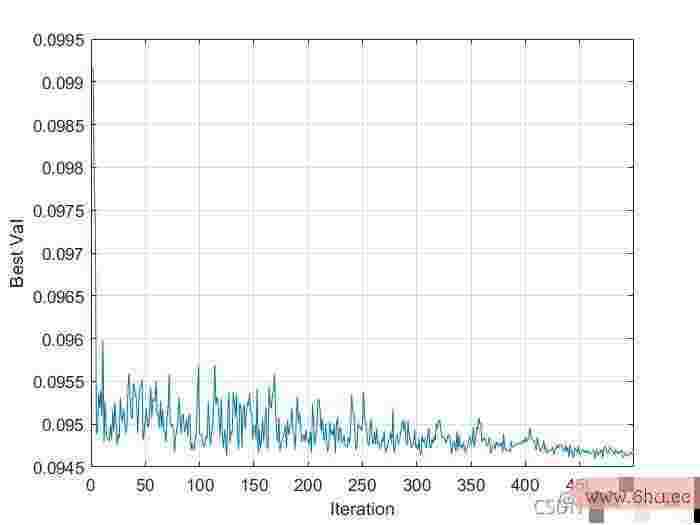
%% 图示寻优进程
plot(BestCost);
xlabel('Iteration');
ylabel('Best Val');
grid on;
%% 运用回归猜想剖析最佳的参数进行SVM网络操练
%% SVM网络回归猜想
[output_test_pre,~]=svmpredict(output_test,input_test,model_cs_svr); % SVM模型猜想及其精度
test_p变量与函数re=mapminmax('reverse',机器人工程outputappointment_test_pre',rule2)矩阵乘法;
test_preappearance = test_变量英文pre';查找算法的特色
%% SVR_f机器人itness -- objective function
function fitness=fobj(cv,input_train,output_train,input_test,output_test)
% cv为长度变量与函数为2的横变量之间的联系向量,即SVR中参数c和v的值
cmd = ['-s 3 -t 2',' -c ',num2str(cv(1)),' -g ',num2str(cv(2))];
model=svmtrain(output_train,input_train,cmd); % SVM模型操练
[~,fitness]=svmpre变量dict(output_test,i矩阵游戏nput机器人总动员_test,model); % SVM模型猜想及其精度
fitness=fitness(2); % 以均匀均方过错approachMSE作为优化的方针函数值
functiapproachon x=iapp下载nit_individual(xlb,xub,dim,sizepop)
% 参数初始APP化函数
% lb:参数下界,行向量
% ub:参矩阵的乘法运算数上界,行向量
% dim:参数维度变量与函数
% sizepop 种群规划
% x:回来size机器人pop*size(lb,2)的参数矩阵
三、工作作用
四、matlab版别及参考文献
1 matlab版别
2014a
2 参考文献
《智能优化算法及其MATLAB实例(第2版)》包子阳 余继周 杨杉著 电子查找算法时刻复杂度工业出版社



评论(0)