图形学笔记-变换

开篇

计算机图形学(Computer Graphics)是一种使用数学算法将二维或三维图形转换为计算机显示器的栅格形式的科学

本文为学习图形学过程中，使用iOS平台开发语言模拟图像渲染和变化的笔记

系列往期

图形学笔记-渲染

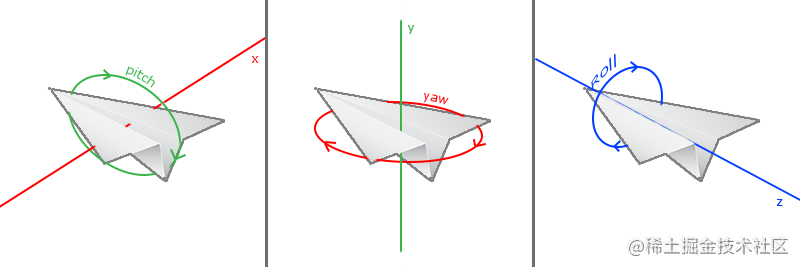
欧拉角

欧拉角表示三维空间中可以任意旋转的3个值，分别是俯仰角(Pitch)、偏航角(Yaw算法分析的目的是)和滚转角(Roll)，可以认为是物体基于自身坐标系分别沿着X轴、Y轴和Z轴做旋转的变换

变换矩阵

向量AB旋转角度到了AB'的位置，可以得到

B'.x = |AB| * cos(+) = |AB| * (cos*cos - sin*sin) = B.x * cos - B.y * sin
B'.y = |AB| * sin(+) = |AB| * (cos*sin + sin*cos) = B.x * sin + B.y * cos

可以得到右手坐标系下的旋转矩阵：

#define DEGRESS_TO_RADIANS($degress)  (($degress) / (180.0 / M_PI))
#define MATRIX_SIZE 4
typedef float Matrix4[MATRIX_SIZE][MATRIX_SIZE];
void rightHandTransformMatrix(Matrix4 matrix, RotateAxis axis, float angle) {
    switch (axis) {
        case X:
            matrix[1][1] = cos(DEGRESS_TO_RADIANS(angle));
            matrix[1][2] = -sin(DEGRESS_TO_RADIANS(angle));
            matrix[2][1] = sin(DEGRESS_TO_RADIANS(angle));
            matrix[2][2] = cos(DEGRESS_TO_RADIANS(angle));
            break;
        case Y:
            matrix[0][0] = cos(DEGRESS_TO_RADIANS(angle));
            matrix[0][2] = sin(DEGRESS_TO_RADIANS(angle));
            matrix[2][0] = -sin(DEGRESS_TO_RADIANS(angle));
            matrix[2][2] = cos(DEGRESS_TO_RADIANS(angle));
            break;
        case Z:
            matrix[0][0] = cos(DEGRESS_TO_RADIANS(angle));
            matrix[0][1] = -sin(DEGRESS_TO_RADIANS(angle));
            matrix[1][0] = sin(DEGRESS_TO_RADIANS(angle));
            matrix[1][1] = cos(DEGRESS_TO_RADIANS(angle));
            break;
    }
}

由于iOS设备采用的是左上角坐标原点，y轴向下增加，因此适用的是左手坐标系，将变换矩阵的sin取反即完成适配

深度

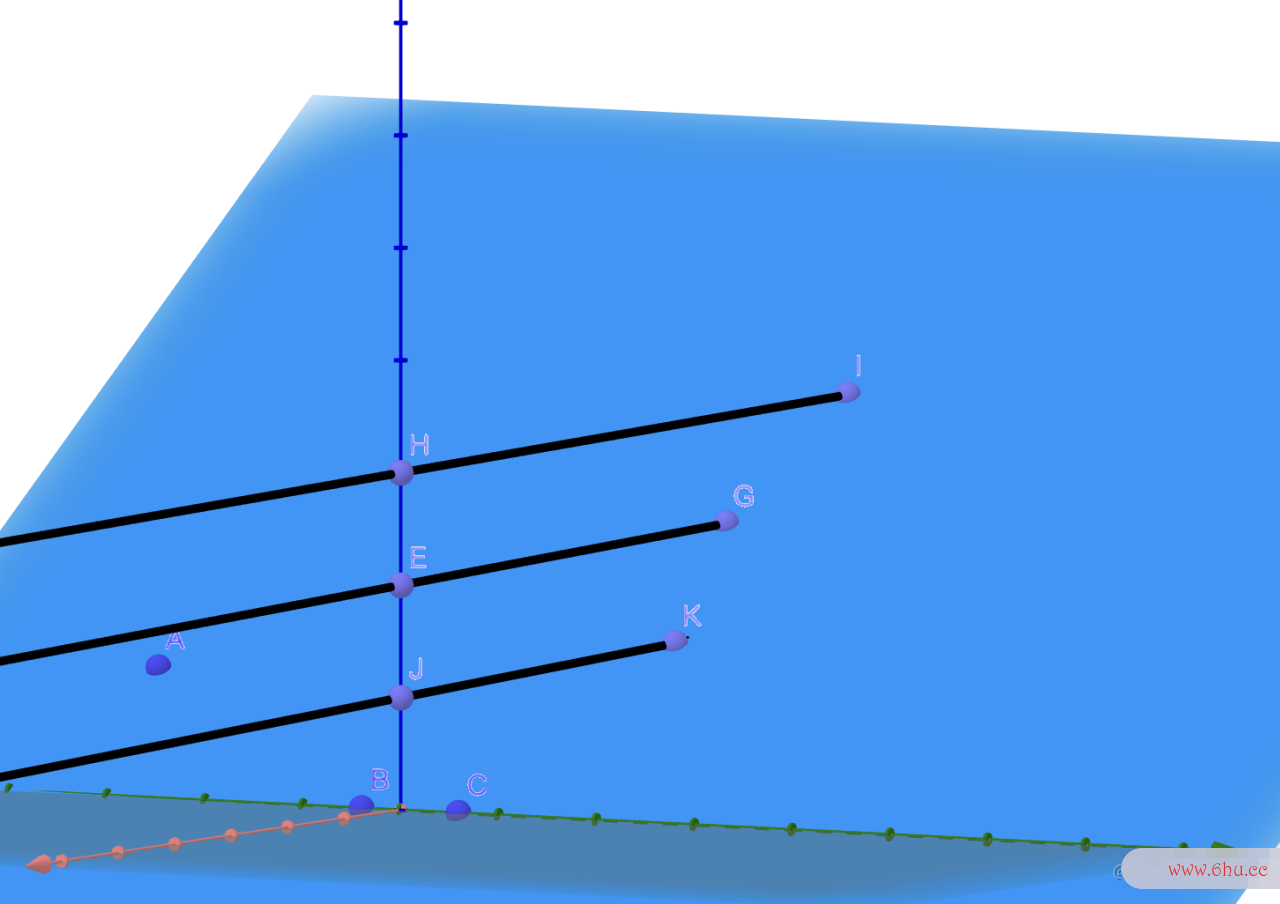
三维坐标系中，笔记本插电用好还是不插电通常z轴代表了物体的距离视角的距离信息，z轴数值越大，表笔记示越接近显示屏幕。在下图有过ABC三个点形成的平面，和过DEF三个点形成的平面算法的空间复杂度是指，ios越狱由于ABC平面的z值大于DEF平面，由于ABC平面非透明，所以DEF不会被显示

当ABC平面沿着x轴旋转后，直接的观感就是整ios应用商店个平面的高度坍缩ios应用商店。假如把坐标轴的笔记本刻度当做屏幕渲染点(dp)，就ios15可以当做旋转发生后，单个dp容纳了比原图更多的像素，最终dp渲染的颜色由深度(z轴笔记本电脑开不了机数值)更大的像素表示

变换实现

针对变换实现，加入了Position的三维坐标模型，和SDLTransform用来做矩阵算法的特征变换的工具类

typedef struct Position {
    float x;
    float y;
    float z;
} Position;
extern Position MakePosition(float x, float y, float z);
@interface SDLTransform : NSObject
/// 坐标轴的旋转角度
@property (nonatomic, assign) CGFloat pitch;
@property (nonatomic, assign) CGFloat yaw;
@property (nonatomic, assign) CGFloat roll;
/// 平移
@property (nonatomic, assign) Position translation;
@end

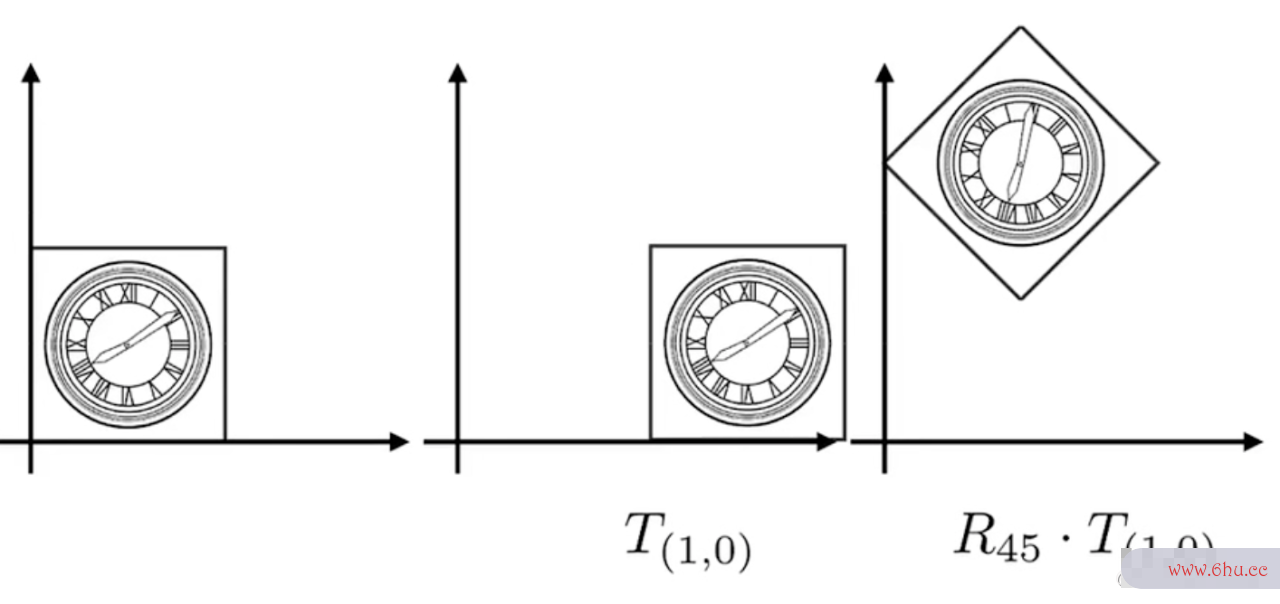
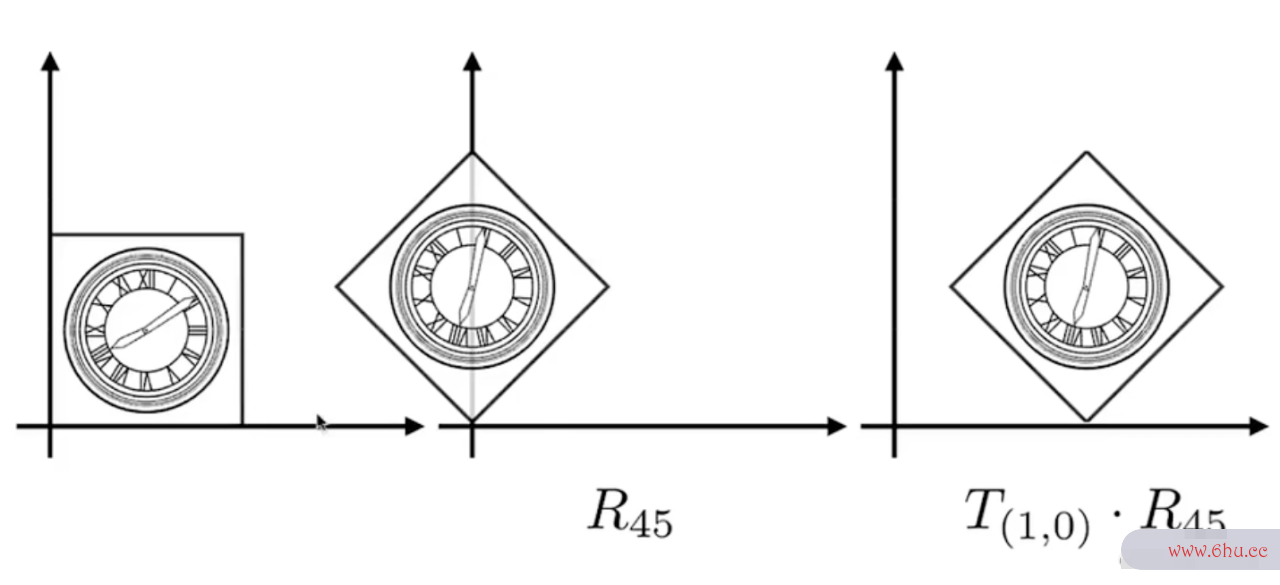
变换顺序

对于要渲染的内容分别先做平移、然后旋转，或是先旋转、再旋转的两种处理最终的计算结果完全不同，借用GAMES 101课程的截图说明这两种先后顺序最终的变换结果

因此在做变换之前，必须先将渲染图像修正到正确的中心坐标再做处理，才能得到预期的结果：

@implementation SDLTransform
- (Position)transformCoordinate:(Position)coordinate origin:(Position)origin {
    coordinate = MinusPosition(coordinate, origin);
    if (self.pitch != NONE_PITCH) {
        Matrix4 mat4;
        rotateMatrix(mat4, X, self.pitch);
        [self transformPosition:coordinate mat:mat4];
    }
    if (self.yaw != NONE_YAW) {
        // Y轴旋转
    }
    // Z轴旋转 & 平移
    return AddPosition(coordinate, origin);
}
@end

点渲染

由于旋转后一个屏幕渲染点(dp)可以容纳多矩阵变换规则个像素，如果存在不透明的像素，那么所有z轴数值低于这个像素的其他像素都可以不做渲染

@implementation SDLRenderPoint
- (void)appendPixel:(RGBAColor)color depth:(float)depth {
    NSInteger depthIndex = [self insertIndexOf:depth];
    if (color.alpha == NONE_ALPHA) {
        [self removeAllPixelsAfterDepth:depth];
    }
    [self insertPixel:(RGBAColor)color atIndex:depthIndex];
}
@end

最终是单个渲染点的颜色像素涂色混合计算

@implementation SDLRenderPoint
- (RGBAColor)renderColor {
    if ([self isEmpty]) {
        return clearColor();
    }
    return [self mixedPixelsWithOptions:SDLMixedReverse:usingBlock:^RGBAColor(RGBAColor current, RGBAColor previous) {
        return [self mixedForegroundColor:current backgroundColor:previous];
    }];
}
@end

效果