梯度下降

丢失函数是衡量模型预估值和实在值差异的衡量，之所以存在差异是因为模型中的参数（比方感知机中的 $w$和$b$）还有待练习，在神经网络中因为参数动辄上亿，假如没有一个战略全凭直觉去调就算到宇宙爆炸也很难优化好。目前常用的战略是反向传达，而梯度下降法便是反向传达中的一种办法，其基本思想是经过迭代的办法，沿着丢失函数的梯度的反方向更新参数，从而逐步逼近函数的最小值。

基本概念

在了解梯度下降的算法之前，咱们先了解下面一些概念。

1. 导数:
   1. 含义： 导数衡量了函数在某一点的瞬时改动率，也便是函数在这一点的斜率。直观地说，导数告诉咱们函数在某点的改动趋势，是在增加仍是减少。
2. 偏导数:
   1. 含义： 当咱们有一个多变量函数时，偏导数表明在一个特定变量的改动方向上的改动率。关于一个二元函数，偏导数便是在其间一个变量上的导数。
3. 梯度:
   1. 含义： 梯度是一个向量（向量有方向和大小），其间每个元素是在对应维度上的偏导。在多变量函数中，梯度指示了函数在某一点上改动最快的方向，沿着梯度向量的方向，愈加简单找到函数的最大值。沿着梯度向量相反的方向，愈加简单找到函数的最小值。
   2. 实践核算比方： 假定有一个二元函数：f(x,y)=x2+5yf(x,y) = x^{2} + 5yf(x,y)=x2+5y，咱们想核算它在点 (1，3)处的梯度。首要核算偏导数：
      ∂f∂x=2x⇒∂f∂x(1,3)=2frac{{∂f}}{{∂x}} = 2 x ⇒ frac{{∂f}}{{∂x}}(1,3)=2∂x∂f​=2x⇒∂x∂f​(1,3)=2
      ∂f∂y=5⇒∂f∂y(1,3)=5frac{{∂f}}{∂{y}} = 5 ⇒ frac{{∂f}}{{∂y}}(1,3)=5∂y∂f​=5⇒∂y∂f​(1,3)=5
      • 梯度$\nabla f$（∇ 读 nabla）便是由偏导数组成的向量：$\nabla f(1，3)=(2，5)$。这告诉咱们在点 (1，3)处，函数改动最快的方向是 (2，5)。
4. 方针函数： 也称为假定函数（hypothesis function），它是为了拟合输入样本的函数。需求拿它跟实在值核算loss。
   1. 回归使命（线性回归）的方针函数是h(x)=0+1×1+…+nxn=∑i=0nixih_{theta}(x)=theta_0+theta_1{x_1}+…+theta_n{x_n} = sum_{i=0}^{n}theta_{i}x_{i}h​(x)=0​+1​x1​+…+n​xn​=∑i=0n​i​xi​
   2. 二分类使命（sigmoid）的方针函数是h(x)=11+e−∑i=1nixih_{theta}(x)=frac{1}{1+e^{-sum_{i=1}^{n}theta_{i}x_{i}}}h​(x)=1+e−∑i=1n​i​xi​1​
   3. 多分类使命：在深度学习中，特别是神经网络的分类层，常运用Softmax函数。关于一个具有K个类别的问题，Softmax 函数将输入的 K 维向量转换为一个表明每个类别概率的 K 维向量。方式如下：Softmax(z)i=ezi∑j=1mezjSoftmax(z)_i=frac{e^{z_i}}{sum_{j=1}^{m}{e^{z_j}}}Softmax(z)i​=∑j=1m​ezj​ezi​​
      1. 其间$z$是输入向量的未归一化分数， Softmax(z)iSoftmax(z)_iSoftmax(z)i​表明第 i 个类别的预测概率。
5. 丢失函数:
   1. 穿插熵丢失函数（Cross-Entropy Loss）：
      1. 定义： 穿插熵是信息论中的概念，用于衡量两个概率散布之间的差异。在神经网络中，穿插熵常用于分类问题。关于二分类问题，丢失函数为二分类穿插熵；关于多分类问题，丢失函数为多分类穿插熵。
      2. 二分类：J()=−(ylog(h(x))+(1−y)log(1−h(x)))J(theta)=−(ylog(h_{theta}(x))+(1−y)log(1−h_{theta}(x)))J()=−(ylog(h​(x))+(1−y)log(1−h​(x)))
      3. 多分类（softmax）： J()=−∑i=1myilog(ai)J(theta) = -sum_{i=1}^{m}y_{i}log(a_i)J()=−∑i=1m​yi​log(ai​)，其间 yiy_iyi​表明第i个分类的实在概率，aia_iai​表明第$i$ 个分类的预估概率（也便是Softmax求出的第 $i$个值）。但在现实中的多分类使命中一般只有一个结果，便是说某一个分类为1其他都为0，假定练习数据的实在输出为第 $j$个为1，丢失函数变成：J()=−log(aj)J(theta) = -log(a_j)J()=−log(aj​)
   2. 均方差丢失函数（Mean Squared Error，MSE）：
      1. 定义： 均方差丢失函数用于回归问题，它衡量实践输出与期望输出之间的平方差。在神经网络中，常用于输出是接连数值的问题。
      2. 公式： J()=12n∑i=1n(yi−h(x)i)2J(theta) = frac{1}{2n}sum_{i=1}^{n}{(y_{i}-h_{theta}(x)i)^{2}}J()=2n1​∑i=1n​(yi​−h​(x)i)2，其间yiy_iyi​表明第$i$个样本的实在值，h(x)ih_{theta}(x)_ih​(x)i​表明第$i$个样本的预估值。
6. 学习率： 每一步沿梯度反方向前进的长度，该参数过大简单越过最优解，过小则收敛速度慢，在实践运用中能够多取一些值，从大到小别离运转算法，调查迭代作用，假如丢失函数在变小说明取值有用，否则要增大步长。

梯度下降法详解

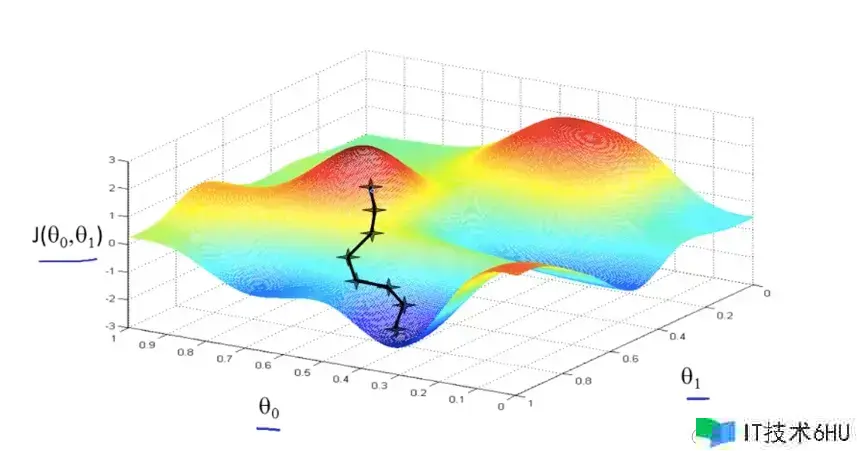
经过上面的介绍，咱们现已对丢失函数有了必定的了解，而且能够沿着梯度的反方向一步步迭代求解，得到最小化的丢失函数，举个下山的比方，人假如要最快下到山底，每一步都沿着当前最陡峭的方向（也便是梯度的反方向）下降，当然这样走下去，有可能咱们不能走到山脚，而是到了某一个局部的山峰低处。

上面的图画（来源：Andrew Ng Machine Learning）是丢失函数$J$的曲面，这里的变量有两个0theta_00​和1theta_11​，所以画出来是三维的，假如有更多的参数则是更高维空间的曲面。

接下来我拿线性回归举例一步步演示怎么经过梯度下降法完成参数的迭代更新。

1. 线性回归的方针函数是h(x)=∑i=1nixih_{theta}(x)=sum_{i=1}^{n}theta_{i}x_{i}h​(x)=∑i=1n​i​xi​，丢失函数是J()=12n∑i=1n(yi−h(x)i)2J(theta) = frac{1}{2n}sum_{i=1}^{n}{(y_{i}-h_{theta}(x)_i)^{2}}J()=2n1​∑i=1n​(yi​−h​(x)i​)2
2. 丢失函数的梯度是：
   ∂J(0,1…,n)∂i=[∂J(0,1…,n)∂0，∂J(0,1…,n)∂1，…，∂J(0,1…,n)∂n]=1n∑j=1n(yj−h(x)j)xi(j)frac{∂J(theta_0,theta_1…,theta_n)}{∂theta_i} = [frac{∂J(theta_0,theta_1…,theta_n)}{∂theta_0}， frac{∂J(theta_0,theta_1…,theta_n)}{∂theta_1}，…，frac{∂J(theta_0,theta_1…,theta_n)}{∂theta_n}] = frac{1}{n}sum_{j=1}^{n}{(y_{j}-h_{theta}(x)_j)}x_i^{(j)}∂i​∂J(0​,1​…,n​)​=[∂0​∂J(0​,1​…,n​)​，∂1​∂J(0​,1​…,n​)​，…，∂n​∂J(0​,1​…,n​)​]=n1​j=1∑n​(yj​−h​(x)j​)xi(j)​

• 注意这里的$j$是第 $j$个样本，xi(j)x_i^{(j)}xi(j)​ 是第$j$个样本的第$i$个特征。
• 当前点的梯度方向是由一切的样本决定的。

1. 有了梯度后就能够结合学习率（步长）去更新 theta参数：i=i−1n∑j=1n(yj−h(x)j)xi(j)theta_{i} = theta_{i} – alphafrac{1}{n}sum_{j=1}^{n}{(y_{j}-h_{theta}(x)_j)}x_i^{(j)}i​=i​−n1​∑j=1n​(yj​−h​(x)j​)xi(j)​
   • 其间 alpha是学习率
2. 假如一切的 theta在当次的下降间隔都小于阈值 epsilon则核算中止。

链式求导

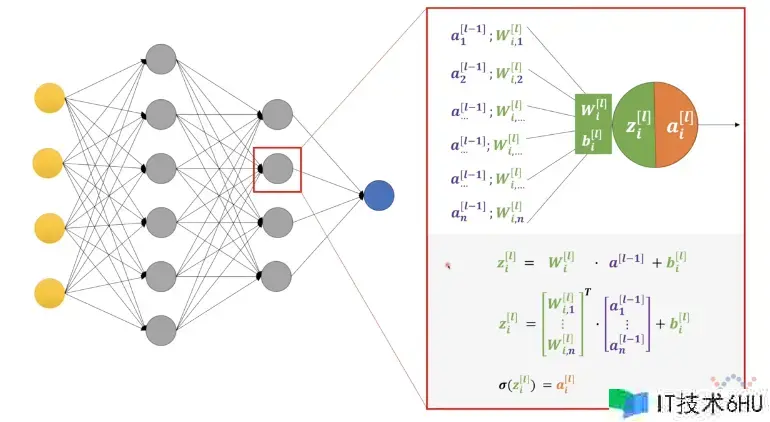
目前比较火的深度神经网络的躲藏层十分多，在如此多层的网络结构中要想完成反向传达就要用到链式求导，从上面这张图中随便选一个感知机，它是由 $w、b、z和a$四部分组成。

• zi[l]=wi[l]∗a[l−1]+bi[l]z_i^{[l]} = w_i^{[l]} * a^{[l-1]} + b_i^{[l]}zi[l]​=wi[l]​∗a[l−1]+bi[l]​
• wil表明第l层的第i个感知机的w参数，因为是全衔接，所以w的个数等于l−1层的感知机数量，即wi[l]可拆解为[wi,1[l],wi,2[l],…,wi,n[l]]w_i^{l}表明第 l层的第 i个感知机的 w 参数，因为是全衔接，所以w的个数等于 l-1层的感知机数量，即 w_i^{[l]}可拆解为 [w_{i,1}^{[l]},w_{i,2}^{[l]},…,w_{i,n}^{[l]}]wil​表明第l层的第i个感知机的w参数，因为是全衔接，所以w的个数等于l−1层的感知机数量，即wi[l]​可拆解为[wi,1[l]​,wi,2[l]​,…,wi,n[l]​]
• a[l−1]则是l−1层的每个感知机的输出。a^{[l-1]}则是 l-1层的每个感知机的输出。a[l−1]则是l−1层的每个感知机的输出。
• bi[l]是第l层第i个感知机的偏置项。b_i^{[l]}是第 l层第 i个感知机的偏置项。bi[l]​是第l层第i个感知机的偏置项。
• 每个感知机的输出ai[l]=(zi[l])a_i^{[l]} = sigma(z_i^{[l]})ai[l]​=(zi[l]​)，其间 sigma是激活函数，作用是非线性变换，进步模型拟合才能。

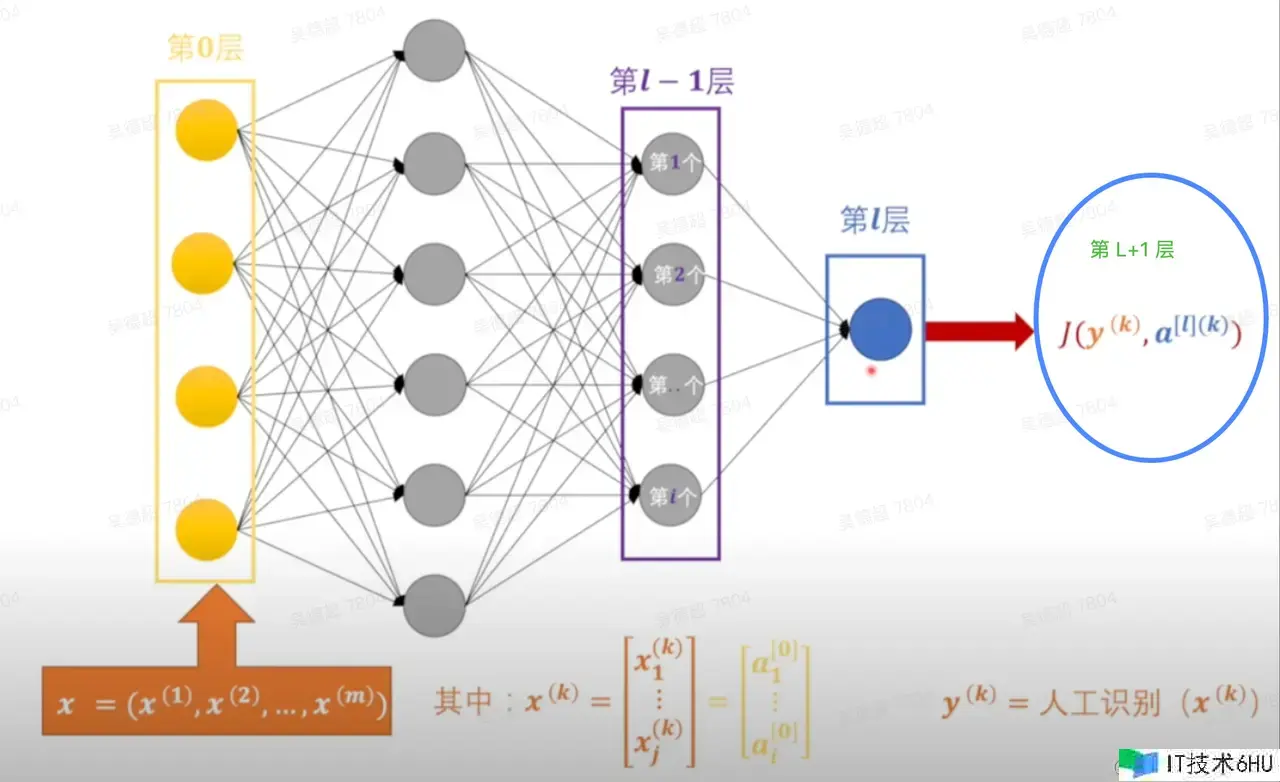
丢失函数 J(y(k),a[l](k))J(y^{(k)}, a^{[l](k)})J(y(k),a[l](k))中的y(k)y^{(k)}y(k)表明第$k$个样本的实在值，a[l](k)a^{[l](k)}a[l](k)表明第$k$个样本的第$l$层的输出（方括号表明网络层，圆括号表明样本）。为了提高了解我把最终的J(y(k),a[l](k))J(y^{(k)},a^{[l](k)})J(y(k),a[l](k))当做第$l+1$层，它的丢失是由第$l$层的输出也便是a[l]a^{[l]}a[l]导致的，此时求第$l+1$层丢失函数$J$的梯度：

• ∇J[l+1]=∂J[l+1]∂a[l]nabla{J^{[l+1]}} = frac{∂{J^{[l+1]}}}{∂a^{[l]}}∇J[l+1]=∂a[l]∂J[l+1]​
• 因为a[l]=(z[l])=(w[l]∗a[l−1]+b[l])a^{[l]} = sigma(z^{[l]}) = sigma(w^{[l]} * a^{[l-1]} + b^{[l]})a[l]=(z[l])=(w[l]∗a[l−1]+b[l])，所以$J$的梯度便是别离对w[l]w^{[l]}w[l]、a[l−1]a^{[l-1]}a[l−1]和b[l]b^{[l]}b[l]求偏导，需求链式求导将其打开，即
  • ∂J[l+1]∂a[l]=(∂J[l+1]∂w[l],∂J[l+1]∂a[l−1],∂J[l+1]∂b[l])=(∂J[l+1]∂∂∂z[l]∂z[l]∂w[l],∂J[l+1]∂∂∂z[l]∂z[l]∂a[l−1],∂J[l+1]∂∂∂z[l]∂z[l]∂b[l])frac{∂J^{[l+1]}}{∂a^{[l]}} = (frac{∂J^{[l+1]}}{∂w^{[l]}},frac{∂J^{[l+1]}}{∂a^{[l-1]}},frac{∂J^{[l+1]}}{∂b^{[l]}}) = (frac{∂J^{[l+1]}}{∂sigma}frac{∂sigma}{∂z^{[l]}}frac{∂z^{[l]}}{∂w^{[l]}},frac{∂J^{[l+1]}}{∂sigma}frac{∂sigma}{∂z^{[l]}}frac{∂z^{[l]}}{∂a^{[l-1]}}, frac{∂J^{[l+1]}}{∂sigma}frac{∂sigma}{∂z^{[l]}}frac{∂z^{[l]}}{∂b^{[l]}})∂a[l]∂J[l+1]​=(∂w[l]∂J[l+1]​,∂a[l−1]∂J[l+1]​,∂b[l]∂J[l+1]​)=(∂∂J[l+1]​∂z[l]∂​∂w[l]∂z[l]​,∂∂J[l+1]​∂z[l]∂​∂a[l−1]∂z[l]​,∂∂J[l+1]​∂z[l]∂​∂b[l]∂z[l]​)
  • 首要$J$先对 sigma求导，sigma再对$z$求导，$z$最终别离对$w、a和b$求导，因为$w$是一个向量，所以对$w$求导便是对其间每个元素求偏导，即：∂J[l+1]∂w[l]=(∂J[l+1]∂w1[l],∂J[l+1]∂w2[l],…,∂J[l+1]∂wi[l])frac{∂J^{[l+1]}}{∂w^{[l]}} = (frac{∂J^{[l+1]}}{∂w_1^{[l]}},frac{∂J^{[l+1]}}{∂w_2^{[l]}},…,frac{∂J^{[l+1]}}{∂w_i^{[l]}})∂w[l]∂J[l+1]​=(∂w1[l]​∂J[l+1]​,∂w2[l]​∂J[l+1]​,…,∂wi[l]​∂J[l+1]​)，$a和b$也是这样就先不打开了。

有了梯度后接下来对参数更新：

.

.

因为∂J[l+1]∂a[l−1]frac{∂J^{[l+1]}}{∂a^{[l-1]}}∂a[l−1]∂J[l+1]​没有办法直接更改，它依靠前面$l-1$层的输出也便是a[l−1]a^{[l-1]}a[l−1]的改动，所以能够把∂J[l+1]∂a[l−1]frac{∂J^{[l+1]}}{∂a^{[l-1]}}∂a[l−1]∂J[l+1]​当做第$l$层丢失函数的值，也便是J[l]=∂J[l+1]∂a[l−1]J^{[l]} = frac{∂J^{[l+1]}}{∂a^{[l-1]}}J[l]=∂a[l−1]∂J[l+1]​，这样就完成了丢失值从$l+1$层到$l$层的传导，整个进程循环迭代起来。

常见梯度下降法

根据更新参数时运用的样本量，梯度下降法能够分为批量、小批量和随机梯度下降法。

1. 批量梯度下降法（BGD）

   • 该办法的标志是运用该batch的一切样本来进行更新：

     i=i−1n∑j=1n(yj−h(x)j)xi(j)theta_{i} = theta_{i} – alphafrac{1}{n}sum_{j=1}^{n}{(y_{j}-h_{theta}(x)_j)}x_i^{(j)}i​=i​−n1​∑j=1n​(yj​−h​(x)j​)xi(j)​

   • 当练习样本量级十分大时，每次参数更新都要运用一切的样本显然会花费较长核算时间，导致整体的练习效率低下，这种办法仅存在理论层面。

2. 随机梯度下降法（SGD）

   • 该办法的标志是从该batch中随机选取一个样本$$j$$来求梯度。对应的更新公式是：

     i=i−(yj−h(x)j)xi(j)theta_{i} = theta_{i} – alpha{(y_{j}-h_{theta}(x)_j)}x_i^{(j)}i​=i​−(yj​−h​(x)j​)xi(j)​

   • 因为每次随机选一个样本核算梯度更新参数，练习速度很快，但因为随机选的样本有必定的不确定性，可能会导致非最优解。

3. 小批量梯度下降法（MBGD）

   • 这种办法是批量和随机两种办法的折中，比方核算一个区域居民的平均身高，现实中不太可能把一切的用户都核算到，而是随机选出一批用户，核算这批用户的平均身高来代表这一区域，更新公式是：

     i=i−1m∑j=1m(yj−h(x)j)xi(j)theta_{i} = theta_{i} – alphafrac{1}{m}sum_{j=1}^{m}{(y_{j}-h_{theta}(x)_j)}x_i^{(j)}i​=i​−m1​∑j=1m​(yj​−h​(x)j​)xi(j)​，其间$m$表明随机选出的$m$个用户。

在实践业务中，假如数据集十分大但内存有限，或者需求处理在线学习问题，那么随机梯度下降可能是一个合适的选择。假如有足够的核算资源，且数据集规划适中，那么能够测验小批量梯度下降甚至批量梯度下降。

最终

经过前面的介绍，我相信大家对梯度下降法有了深化的了解。在实践运用中，咱们一般对模型的练习和收敛速度有着较高的要求。除了前面提到的从样本集大小的角度考虑，还有一些优化办法能够在提高收敛速度方面发挥重要作用，其间包含动量法、Adagrad、RMSprop 和 Adam 等。

在接下来的文章中，我将深化介绍梯度下降中的各类优化改善办法，以帮助大家更好地了解怎么调整模型的练习进程，进步练习效率。敬请期待。