刹车与油门：PyTorch Autograd 的赛车之旅

关于大模型的学习与探索不要停止，LLM 就是“未来已来”。

前面经过简略的实操上手 Pytorch：# 轻松上手：PyTorch 猜测书店销售趋势，本篇带来 Pytorch 中心引擎：autograd。

那么，autograd 在 Pytorch 中是怎样的定位呢？

一句话：autograd 为 Tensors 上的一切操作供给主动微分。 用白话来作比方：

神经网络经过不断调整参数（类似于轿车的油门），微分是告知网络：假如你稍微调整一下参数，猜测值会怎么改变（轿车速度仪表盘）。

当你加快时，仪表盘速度逐步增加；而当你减速时，仪表盘速度逐步减小。这个速度的改变信息，就比如微分供给的导数信息。

autograd像是轿车的智能驾驭体系：它能够主动追寻神经网络中各个参数的改变，同时告知你，每个参数的细小调整会对终究猜测成果发生怎样的影响。

有了autograd，使得咱们能够以一种更智能的方式来训练神经网络，让它逐步学会正确的使命。

详细怎么实践呢？

简略核算

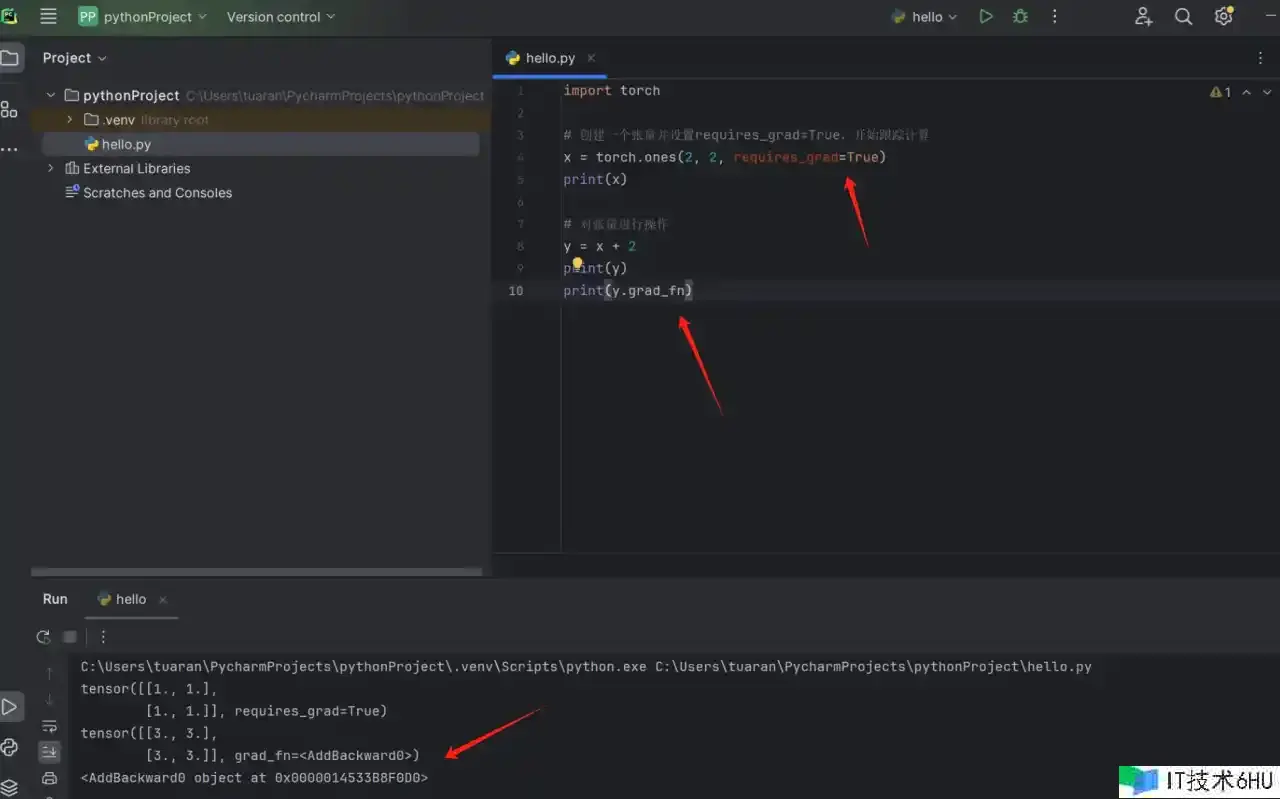
还记得：torch.Tensor张量？经过将特点.requires_grad设置为True，就能实现开端盯梢针对张量的一切操作。

完成核算后，再调用.backward()来主动核算一切梯度，并将梯度累积到.grad特点中。

咱们先设置特点、然后打印看看：

import torch
# 创立一个张量并设置requires_grad=True，开端盯梢核算
x = torch.ones(2, 2, requires_grad=True)
print(x)
# 对张量进行操作
y = x + 2
print(y)
print(y.grad_fn)

y.grad_fn 显示 <AddBackward0 object at ...>。这表明 y 是经过加法操作得到的；

梯度核算

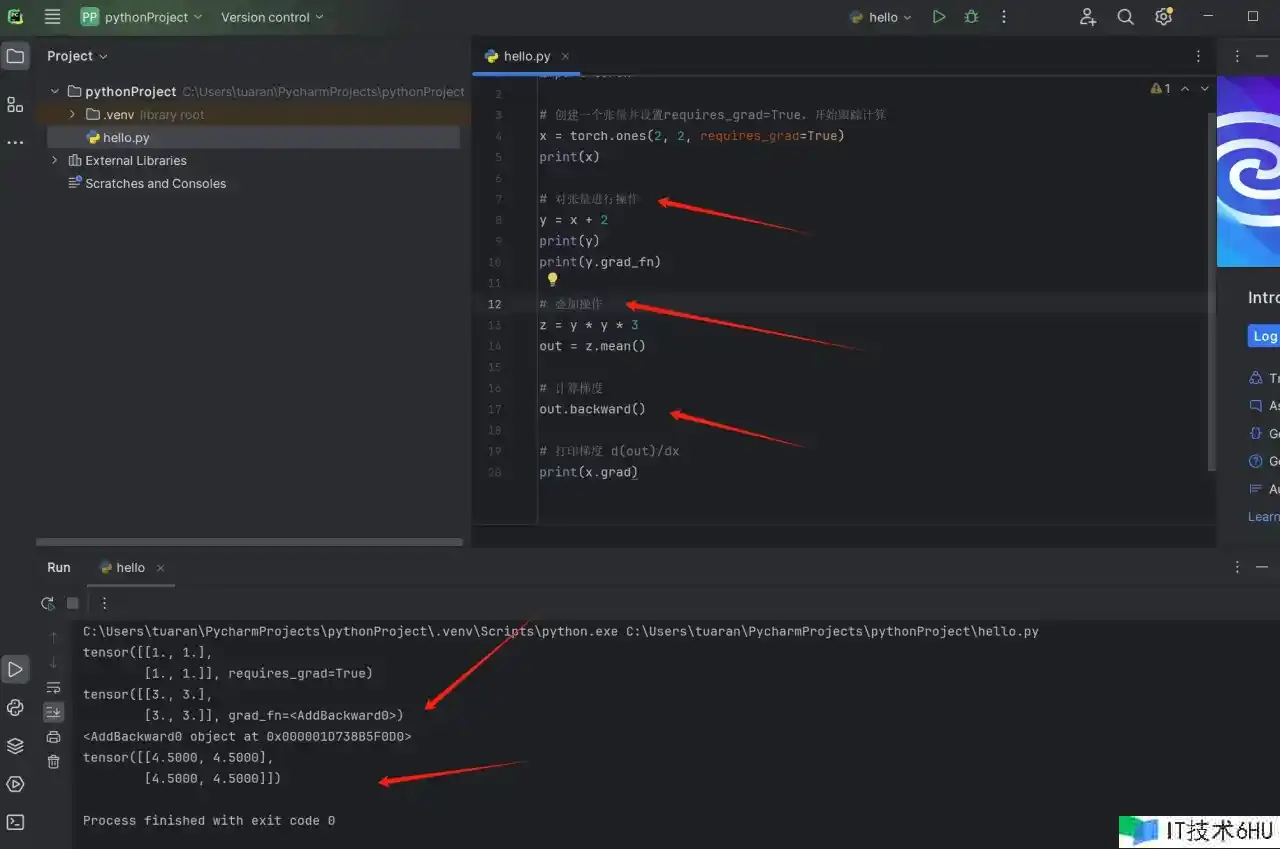
根据以上，再叠加一个乘法核算，然后来核算梯度：

import torch
# 创立一个张量并设置requires_grad=True，开端盯梢核算
x = torch.ones(2, 2, requires_grad=True)
print(x)
# 对张量进行操作
y = x + 2
print(y)
print(y.grad_fn)
# 叠加操作
z = y * y * 3
out = z.mean()
# 核算梯度
out.backward()
# 打印梯度 d(out)/dx
print(x.grad)

调用 out.backward() 表明核算 out 相关于一切具有 requires_grad=True 的张量的梯度；

终究，打印了 x 相关于 out 的梯度，d(out)/d(x)；

拉力竞赛

且慢，假如觉得上述不太好理解， 咱们用“开车”比方：

你参加了一场拉力赛，目标是尽量快地开车冲过终点（out），整个竞赛路途是由一系列拉力赛中的弯道和直道组成。

1、 起点（x）： 你的车停在起点，表明竞赛的初始状态，就是在竞赛开端前的你的方位。

2、榜首段直道（y = x + 2）： 你沿着榜首段直道加快行进，表明进行了一个加法操作，像是在拉力赛中的一段平稳的直道，你能够提速。

3、弯道（z = y * y * 3）： 进入弯道，表明进行平方和乘法操作；弯道可能有些弯曲，需要经过奇妙的驾驭技巧来维持速度。

4、 终点（out = z.mean()）： 终究，你冲过了竞赛的终点，这就是整个核算进程的成果。

竞赛的进程中，你会考虑一个问题：假如我在这个方位采纳稍微不同的战略，我的竞赛时刻会有多大的改变？

这种改变就是梯度，它告知你在每个方位上应该怎么调整你的驾驭战略，以便更快地冲过终点。

将上述代码调整一下：

import torch
# 创立一个张量并设置requires_grad=True，开端盯梢核算
x = torch.ones(2, 2, requires_grad=True)
print("竞赛开端方位 x：", x)
# 进入榜首段直道
y = x + 2
print("进入榜首段直道 y：", y)
print("y 的梯度（直道的加快度）：", y.grad_fn.next_functions[0][0].variable.grad)
# 进入弯道
z = y * y * 3
out = z.mean()
# 核算梯度
out.backward()
# 打印梯度 d(out)/dx
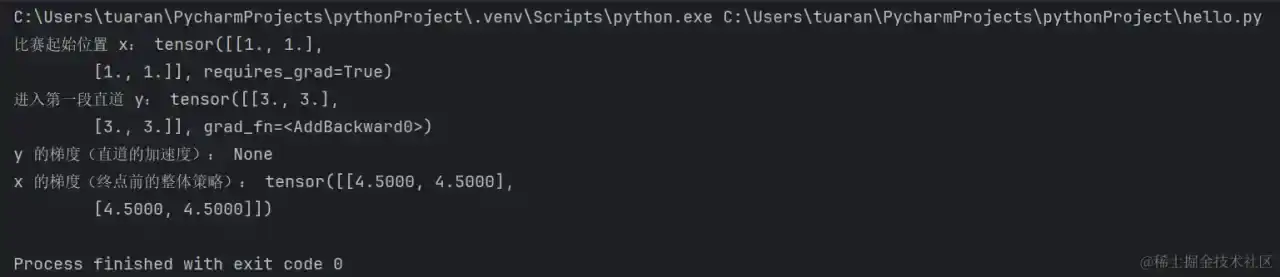
print("x 的梯度（终点前的整体战略）：", x.grad)

运转成果：

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

这表明在整个拉力赛竞赛中，假如在每个方位微调 x 的值，对终究成果的影响。

比如，取张量的左上角元素，其值为 4.5。这表明假如在起点方位微调拉力赛车的某个战略，比如调整油门或方向盘，将会使竞赛成果 out 增加 4.5。同理，其他方位的元素也表明了在对应方位上微调 x 对终究成果的影响。

微调展现

根据上述理论上的原理，咱们则能够开端一定程度的微调了，再凭借 Matplotlib 库制作曲线图；代码如下：

import torch
import matplotlib.pyplot as plt
# 创立一个张量并设置requires_grad=True，开端盯梢核算
x = torch.ones(2, 2, requires_grad=True)
# 存储梯度和成果的改变
grad_history = []
out_history = []
# 进行微调并记载成果改变
for i in range(50):
    # 进入榜首段直道
    y = x + 2
    # 进入弯道
    z = y * y * 3
    out = z.mean()
    # 记载梯度和成果
    if x.grad is not None:
        grad_history.append(x.grad.view(-1).numpy().copy())
    out_history.append(out.item())
    # 核算梯度
    out.backward()
    # 依据梯度微调 x，模仿优化进程
    with torch.no_grad():
        x -= 0.1 * x.grad if x.grad is not None else 0  # 这儿运用一个简略的学习率
    # 清零梯度，以便下一次核算
    x.grad.zero_()
# 制作曲线图
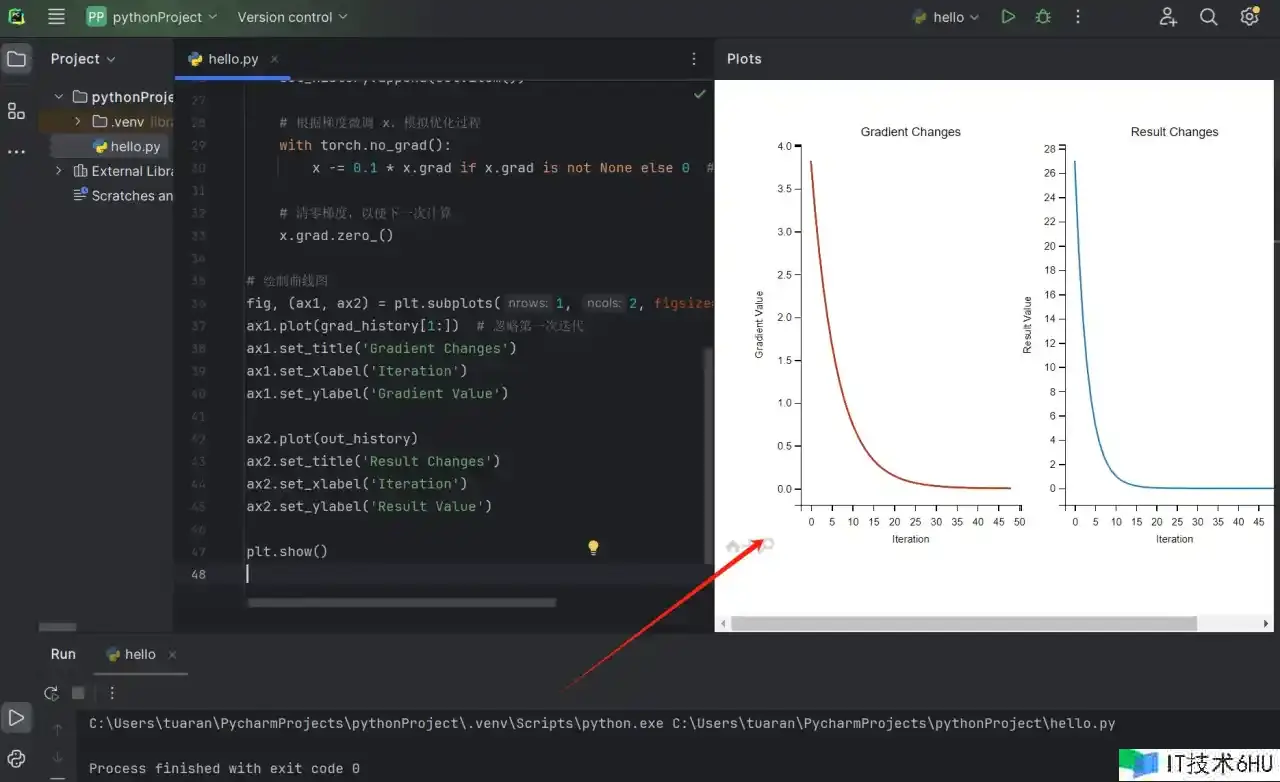
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(grad_history)
ax1.set_title('Gradient Changes')
ax1.set_xlabel('Iteration')
ax1.set_ylabel('Gradient Value')
ax2.plot(out_history)
ax2.set_title('Result Changes')
ax2.set_xlabel('Iteration')
ax2.set_ylabel('Result Value')
plt.show()

1. 创立张量和盯梢核算：

   x = torch.ones(2, 2, requires_grad=True)
   

   先创立了一个2×2的张量 x，并告知PyTorch咱们期望追寻它的核算历史，因为咱们将在优化进程中对它进行微调。

2. 初始化存储变量：

   grad_history = []
   out_history = []
   

   初始化两个空列表，用于存储梯度和成果的改变。

3. 进行微调并记载改变：

   for i in range(50):
       y = x + 2
       z = y * y * 3
       out = z.mean()
   

   在这个循环中，模仿一个简略的优化进程。首先，咱们进入了一个“直道”（y = x + 2），然后进入了一个“弯道”（z = y * y * 3）。out是成果的均值。

4. 核算梯度：

       out.backward()
   

   经过调用 backward() 办法，PyTorch 主动核算了关于 x 的梯度。这个梯度告知咱们在当前参数设置下，丢失函数关于参数的改变方向和强度。

5. 记载梯度和成果：

       if x.grad is not None:
           grad_history.append(x.grad.view(-1).numpy().copy())
   out_history.append(out.item())
   

   咱们将梯度（经过一些处理以方便绘图）和成果的值记载到相应的列表中。

6. 依据梯度微调参数：

       with torch.no_grad():
           x -= 0.1 * x.grad if x.grad is not None else 0
   

   这儿运用一个简略的学习率（0.1）依据梯度微调张量 x，模仿优化算法的一次迭代。

7. 清零梯度：

       x.grad.zero_()
   

   为了保证下一次核算的梯度是根据新的微调后的参数，咱们在每次迭代之后都将梯度清零。

8. 制作曲线图：

   fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
   ax1.plot(grad_history[1:])  # 忽略榜首次迭代
   ax1.set_title('Gradient Changes')
   ax1.set_xlabel('Iteration')
   ax1.set_ylabel('Gradient Value')
   ax2.plot(out_history)
   ax2.set_title('Result Changes')
   ax2.set_xlabel('Iteration')
   ax2.set_ylabel('Result Value')
   plt.show()
   

从左图咱们能够观察到，刚开端梯度值较大，表明在微调的初期，模型参数需要较大的调整。跟着微调的进行，梯度值逐步减小，阐明模型参数逐步挨近最优点。当梯度值挨近零时，阐明模型参数已经趋于稳定，微调的起伏逐步减小。

OK，以上，经过运用一个简略的学习率来微调模型参数，演示了学习率对优化进程的影响。

运用 PyTorch 的主动微分功用 Autograd，就能够轻松地核算模型参数的梯度，而不需要手动推导梯度公式啦~~

OK，以上就是本次共享，期望各位喜爱~ 欢迎点赞、收藏、谈论 我是安东尼 人气技术博主 坚持千日更文 ✍ 重视我，安东尼陪你一起度过漫长编程年月