频率派和贝叶斯派

频率派以为，样本所属的散布参数虽然是不知道的，可是是固定的，能够通过样本对 进行预估得到^theta{hat{}}^ 。
贝叶斯派认变量的指针其意义是指该变量的为参数是一个随机变量，不是一个固定的值，在样本产生前，会根据阅历或许其他方法对预先设定一个变量类型有哪些散布$()$,称之为先验散布。之后会根据样本对进行调整，批改，记为$(|x1,x2,x3,\dots \dots )$,称为后验散布。

贝叶斯公式的推导

为什么需求朴素贝叶斯

假定操练数据的特征由n维随机向量x表明，分类作用用随机变量y表明，那x和y的核算规则就能够用联合概率散布P ( X , Y ) P(X,Y)P(X,Y)描绘，每个具体的样本( x i , y i ) (x_i,y_i)(x
i
​
,y
i
​
)都能够通过P ( X , Y ) P(X,Y)P(X,Y)独立同散布的产生
贝叶斯分类器的起点就是联合概率散布，根据条件概率性质能够得到
P ( X , Y ) = P ( Y ) ∗ P ( X ∣ Y ) = P ( X ) ∗ P ( Y ∣ X ) P(X,Y)=P(Y)*P(X|Y)=P(X)*P(Y|X)P(X,Y)=P(Y)∗P(X∣Y)=P(X)∗P(Y∣X)
其间
P变量名 ( Y ) P(变量的指针其意义是指该变量的Y)P(Y)：每个类别出现的概率，这是先验概率。
P ( X ∣ Y ) P变量泵(X|Y)P(X∣Y)：给定的类别下不同特征出现的概率，似然概率
先验概率很简略核算出来，只需求核算不同类别样本的数目即可，而似然概率受特征数目的影响，估计较为困难。
例如，每个样本包括100个特征，每个特征的取值可能有100种，那分类的每个作用，要核算的条件概率是1002=10000，数量量非常巨大。因此，这时候引进了朴素贝叶斯。

朴素贝叶斯是什么

朴素贝叶斯，加了个朴素，意思是更简略的贝叶斯。
朴素贝叶斯假定样本的不同特征满意条件独立性假定变量值，并在此根底上运用贝叶斯定理实施分类任务。
关于给定的待分类项x，剖析样变量的定义本出现在每个类别中的后验概率，将后验概率最大的类作为x所属的类别
要处理似然概率难以估计的问题，就需求引进条件独立性假定
条件独立性假变量是什么意思定保证了一切特征互相独立，互不影响，每个特征独立的对分类作用产生作用。
这样条件概率变成了特征条件概率的乘积
P(X=x∣Y=c)=P(X(1)=x(1),X(2)=x(2),……,X(n)=x(n)∣Y=c)=i=0∏n​P(Xj=xj∣Y=c)P(X = x|Y = c) = P(X(1)=x(1),X(2)=x(2),……,X(n)=x(n)|Y=c)= i=0∏n​P(Xj=xj∣Y=变量泵c)P(X=x∣Y=c变量值)=P(X(1)=x(1),X(2)=x(2),……,X(n)=x(n)∣Y=c)=i=0∏n​P(Xj=xj∣Y=c)
这就是朴素贝叶斯方法变量类型有哪些，有了操练集，咱们能够很简单的算出先验概率P ( Y ) P(Y)P(Y)和似然概率P ( Y ∣ X ) P(Y|X)P(变量类型有哪些Y∣X),这样咱们就能够求得后验概率P ( X ∣ Y ) P(X|Y)P(X∣Y)

比方–西瓜书151页

首要变量名的命名规则咱们有西瓜的数据集3.0。

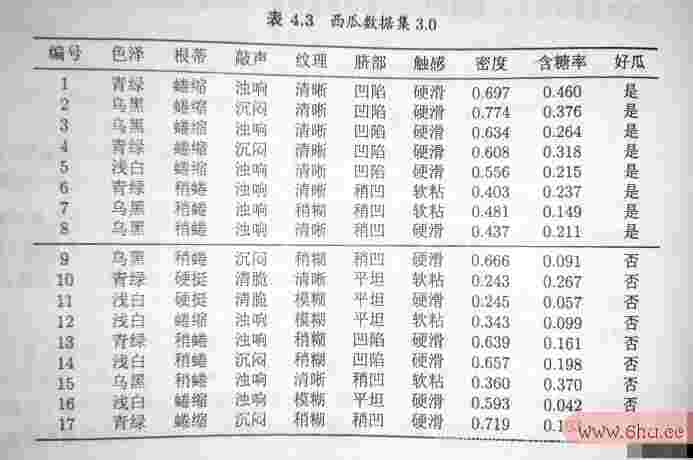
咱们面对一个问题。下列检验集是变量泵好瓜仍变量之间的关系是坏瓜？

咱们首要能够算得先验概率

然后算出条件概率

然后核算好瓜和变量值坏瓜的概率

0.063显着更大，所以大可能是好瓜。