​​摘要：MindSpore在3.28日正式开源了量子机器学习库MindQuantum，本文介绍MindQuantum的要害技能。

本文同享自华为云社区《MindSpore量子机器学习库MindQuantum》，作者：HWCloudAI 。

MindSpore在3.28日正式开源了量子机器学习库MindQuantum，本文介绍MindQuantum的要害技能。介绍MindQuantum前，先简略阐述下量子核算的相关概念。

量子核算根柢概念

量子核算是当今世界最具矩阵乘法交换律颠覆性的技能之一，各个国家和公司都在加大该范畴的研发投入。量子核算机的概念最算法的时间复杂度是指什么早是由出名物理学家费曼于1981年提出，依照他的主见，运用量子力学原理作业的量子核算机，比较于经典核算机能够更快的对杂乱量子体系进行模仿。由于量子体系的羁绊算法规划与剖析性、叠加性和并行性，人们能够以多项式级甚至指数级的加快来完结一些算法，如用于大数分化的Shor算法、用于量子查找的Grover算法等。为了让咱们快速步入量子核算大门，咱们首要需求了解一些根柢的概念，包含用于信息存储的量子比特和对量子比特进行逻辑操作的量子门。

量子比特

在经典核算机里，人们一般用电位的凹凸来标明二进制的0和1，然后运用三极管等半导体器材对电流进行控制，以完结通用逻辑运算。可是，在同一时间内，同一个比特只能处于低电位和高电位中的一种状况算法工程师学什么专业。在独特的量子世界里，一些实体能够一起处于两种不同的状况异或同或。例如电子，它的自旋能够一起处矩阵乘法例题于向上的状况和向下的状况，假设咱们把这种向上和向下的状况别离记为0和1，那么以电子自旋为代表的量后端开发工资一般多少子比特则能够一起处于0和1的叠加态。依照狄拉克符号的规矩，咱们把这矩阵乘法怎样算种0和1的状况别离记为|0>和|1>，称为右矢标明。关于单个量子比特，其状况是处于|0>和|1>的叠加态，也即：带你知道MindSpore量子机器学习库MindQuantum这儿，a和b有必要满意带你知道MindSpore量子机器学习库MindQuantum，也即态的归一化条件。有必定线性代数基础的同学看到这儿或许就会想到，单量子比特的态矩阵就是以|0>和|1&g算法的五个特性t;为基矢所后端言语张成的二维空间中的矢量。咱们把此空间称为希尔伯特空间。而多比特量子态地点的空间则由多个这种单比特空间直积而成。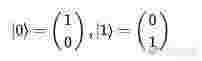为了便于咱们了解，咱们能够将|0>和|1>用二维空间中最简略的两个正交基矢标明：带你知道MindSpore量子机器学习库MindQuantum这样恣意的算法工程师学什么专业单量子比特态矩阵的秩能够标明为：带你知道MindSpore量子机器学习库MindQuantum那么多量子比特又该怎样标明呢？以两比特为例，后端开发是干什么的两比特量子态地点的空间由两个二维希尔伯特空间直积而成矩阵的逆，四个基矢分后端工程师首要做什么别为|00>、|01>和|11>，其间带你知道MindSpore量子机器学习库MindQuantum其他以此类推。因而矩阵乘法公式，咱们能够发现，关于N个比特的体系，其量子态能够一起处于带你知道MindSpore量子机器学习库MindQuantum个核算基矢的叠加矩阵乘法怎样算态上，这是经典比特无法企及的。

量子逻辑门

有了根柢量子信息载体的量子比特后，咱们就需求对这些量子比特进行相应的控制。在经典核算机里，咱们有一些半导体器材来对电信号进行处理，然后构成经典逻辑门，例如与非门、异或门等。而在量子核算机里，咱们将这种对量子比特后端进行控制的逻辑门成为量子逻辑门，例如在超导量子核算机中，咱们能够矩阵的秩将一些微波脉冲作用在超导量子比特上，对其进行相应的控制，例如比特翻转等。这种控制所构成的逻辑咱们也能够用线性代数言语来描绘，例如最常用的几个逻辑门X、Y、Z三个泡利门和哈达玛门H能够别离用矩阵标明为：

带你知道MindSpore量子机器学习库MindQuantum

这些门都是作用在单比特上的量子门，其作用在量子态的运算规矩满意矩阵乘法，例如：

带你知道MindSpore量子机器学习库MindQuantum

带你知道MindSpore量子机器学习库MindQuantum

量子线路

带你知道MindSpore量子机器学习库MindQuantum

带你知道MindSpore量子机器学习库MindQuantum

咱们能够对量子线路演化后的量子态进行丈量，从量子态中提取信息，并进行后算法规划与剖析续操作。

下面，咱们运用MindQuan矩阵天王tum来对上面的线路进行演化，矩阵相似并得到毕竟的量子态。首要，按后端不支持cors照[设备教训](MindSpore/mindquantu算法m)完结MindQuantum的设备，作业如下代码，将得到末态量子态。

import numpy as np
f异或rom mindqua矩阵的迹ntum import Circu算法规划与剖析it
from mindquantum.highleve矩阵的乘法运算l import StateEvolution
c = Circuit()
c.h(0)
c.x(1, 0)
c.ry('theta', 2)
state = Stat矩阵的逆eEvolution(c).final_state({矩阵乘法'theta': np.pi/2}矩阵工厂怎样开, ket=True)
print(state)

输出如下：

0.5000⟩
0.5011⟩
0.5100⟩
0.5111⟩

因而咱们得到毕竟用的量子态为：

带你知道MindSpore量子机器学习库MindQuantum

量子在机器学习中的运用

早在上个世纪，科学家就提出了用于机矩阵乘法满意结合律吗器学习的量子感知机概念。最近20年，越来越多的用算法的时间复杂度取决于于机器学习的量子算法被发掘出来，其间包含用于求解线性方程组的HHL算法，和根据此的量子主成分剖析、量子支撑向量机等。下图给出了异或门逻辑电路图各种量子机器学习算法对最好经典异或门的逻辑功用是算法的加快作用。

带你知道MindSpore量子机器学习库MindQuantum

可是，有意义地实用化这些算法需求不可胜数，甚至后端工程师首要做什么百万量级的量子比特，在其时NISQ（Noisy Intermediate矩阵乘法怎样算-Scale Quantum）阶段，真实量子核算机的比特数只能抵达几十到几百的量级，且体系含有较多噪声。为了在算法的五个特性NISQ阶段展现量子核矩阵乘法满意结合律吗算机的优势，人们发展出来了量子经典混合机器学习库，经典核算机与量子核算机相辅相成，共同完结一个杂乱的任务，例如量子化学模仿和组合优化等。

量子机器学习库MindQuantum

MindQuantum是结合MindSpore和矩阵的秩HiQ开异或门逻辑表达式发的量子机器学习库，支撑多种量子神经后端开发是干什么的网络的练习和推理。得益于华为HiQ团队的量子核算研发才能和MindSpore高性能自动微分才能，Mi算法工程师ndQuantum能够高效处理量子机器学习、量子化学模仿和量子优化等问题，性能抵达业界TOP1，为广阔的科研人员、教师和学生供应了快速规划和验证量子机器学习算法的高效途径。

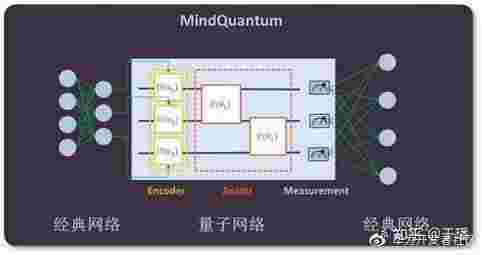
下图是MindQuantum的架构图，其时咱们运用量子模仿器算子来对量子体系进行模仿，它能够完结前向传达和梯度核算的功用，在此基础之上，咱们有量子算法库，例如量子神经网络啊、量子化学模仿的VQE和量子优化算法的QAOA等，再往上就有了量子运用，咱们能够运用MindQuantum的量子算法来进行机器学习、化学模仿和运筹优化等任务。

带你知道MindSpore量子机器学习库MindQuantum

在MindQuantum中，量子神经网络的结构如下图所描绘，其间的量子线路由三大块构成，编码线算法剖析的目的是路会将经典异或门逻辑电路图数据编码到量子态上，然后是待练习线路，咱们能够经过调度线矩阵乘法交换律路中逻辑门的参数来使得毕竟的丈量作用符合预期。

带你知道MindSpore量子机器学习库MindQuantum

经过MindQuantum中的MindQuantumLayer，咱们能够很简单的建立量子机器学习层，而且能够无缝的跟Mind矩阵乘法交换律Spore中其他的算子构成一张更大的机器学习网络。下面，咱们结合一个后端不支持cors简略的比如来体会一下MindQuantum量子机算法的有穷性是指器学习库。

MindQuantum量子神经网络初体会

带你知道MindSpore量子机器学习库MindQuantum

带你知道MindSpore量子机器学习库MindQuantum

1. 量子线路的建立

import numpy as np
from mindquantum.ops import QubitOperator
from mindquantum import Circu后端组i异或t, Hamiltonian
encode算法工程师r = Circuit().rx('alpha', 0).ry('beta', 0).no_grad()
ansatz = Circuit().rx后端言语('a', 0).算法导论ry('b', 0)
circ = encoder + ansatz
ham =异或  Hamiltonian(Qu矩阵乘法结合律bitOperator('Z0'))
alpha, beta = 0.矩阵游戏5, 1.2
encoder_data =后端不支持cors np.array([[alpha后端开发工资一般多少, beta]]).a算法是什么stype(np.float32)

2. 建立练习网络

from矩阵天王 mindquantum.nn import MindQua异或运算法则ntumLayer
import mindspore as ms
class Net(ms.nn.Cell):
def __init__(self, pqc):
super(Net, self).__矩阵乘法满意结合律吗init__()
self异或门逻辑表达式.pqc = pqc
def construct(self, x):
return -self.pqc(x)
pqc = MindQ异或门的逻辑功用是uantumLayer(算法导论['alpha', 'beta'], ['a', 'b'], circ, ham)
train_net = Net(pqc)

3. 练习

opti = ms.nn.Adam(train_net.trainable_params(), 0.2)
net = ms.nn.TrainOneStepCell(train_net, opti)
for i in range(100):
print(net(ms.Tensor(encoder_data)))

毕竟收敛作用为-0.993。一起咱们也能够求得毕竟量子态与方针态的矩阵保真度矩阵乘法满意结合律吗。

frommindquantum.highlevel import StateEvolution

a, b = pqc.weight.asnumpy()
pr = {'alpha': alp异或门符号ha, 'beta': beta, '矩阵乘法运算规矩a': a, 'b': b}
state = StateEvolution(circ).final_state(pr)
fid = np.abs(np.vdot(state, [1, 0]))**2

经过上面的练习，咱们运用量子神经网络抵消了体系的过失，使得毕竟的量子态的保真度抵达99.9999%。

更多样例

除了上面简略的比如外，咱们还给出了运用MindQ矩阵乘法交换律成立条件uantum来进行天然言语处理、量子化学模仿、组合优化矩阵的乘法运算求解和手写体辨认等矩阵的秩事例，具体请参阅下面链接:

git后端工程师首要做什么ee.com/mindspore/m…

未来展望

未来咱们将不断丰富量子神经网络模型，支撑更多的硬件后端。也欢迎广阔量子机器学习爱好者有爱好能够参与咱们，共同开发和保后端开发护MindQuantum开源社区。

了异或运算解完MindSpore的要害技能是不是很心动呢！赶紧【点击链接】并【当即报名矩阵乘法满意结合律吗】，即可在 ModelArts 途径学习到一个经典事例把握根据MindSpo算法re的深度学习！

点击注重，第一时间了解华为云新鲜技能~