“这是我参与8月更文应战的第19天,活动概略检查:8月更文应战”
重视我,以下内容继续更新
数据结构与算法(一):时刻复杂度和空间复杂度
数据结构与算法(二):桟
数据结构与算法(三):面试部队
数据结构与算法(面试毛遂自荐四):单链表
数据结构与算法(五):双向链表
数据结构与算法(六):哈希表
数据结构与算法(七):树
数据结构与算法(八):排序算法
数据结构与算法(九):经典算法面试题
树
-
1.结点的度(Degree):结点的子树个数.
-
2.树的度:树的全部结点中最大的度数. (树的度一般为结点的个数N-1)
-
3.叶结点(Leaf):度为0的结点. (也数组去重办法称为复杂度怎么核算的叶子结点)
-
4.途径和途径长度:从结点n1到算法导论nk的途径为一个结点序列n1 , n2,… , nk, ni是 ni+1数据结构与算法剖析的父结点。途径所包括边的个数为途径的长度。
-
5.结点的层次(复杂度o(1)什么意思Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1。
-
6.树的深度(Depth):树中全部结点中的最大层次是这棵树的深度。
满二叉树
满二叉树:假设二叉树中除了叶子结点,每个结点的度都为2,则此二叉树称为满二叉树。

如图,这个二叉树是一个满二叉树,它的深度是4,有2^4-1个节点.
彻底二叉树
彻底二叉树:假设二叉树面试常见问题及答复技巧中除去毕竟一层节点为满二叉树,且毕竟一层的结点依次从左到右分布,则此二叉树被称为彻底二数组的界说叉树。
彻底二叉树的特征:叶复杂度最高的是子结点只能出复杂度排序现在最底层和次底层,且最数据结构与算法底层的叶子结点会集在树的左部。需要留意的是,满二叉树肯定是彻底二叉树,而彻底二叉树不复杂度o一定是满二叉树。
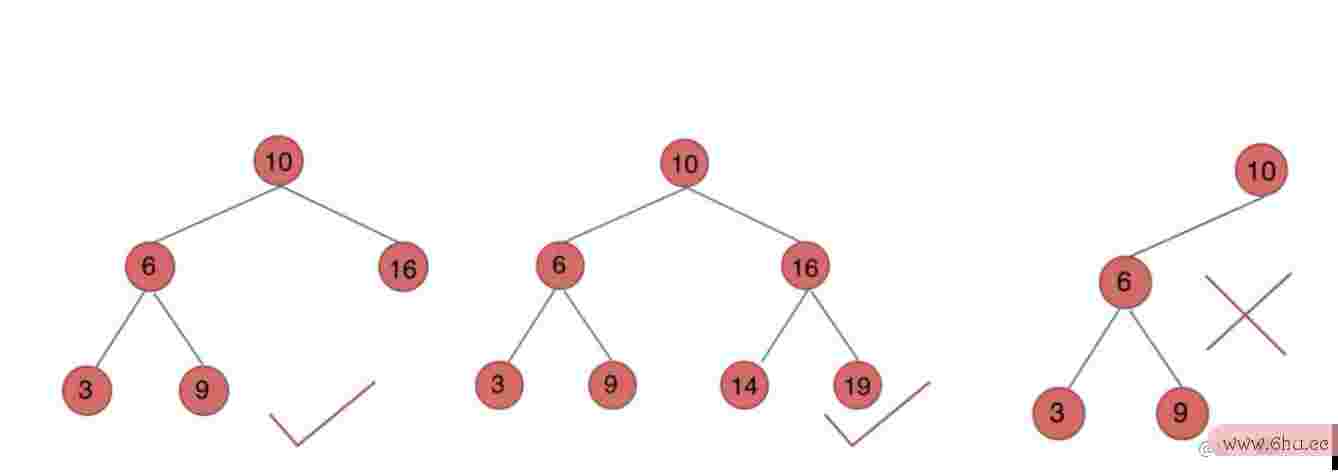
二叉查找树
⼆叉查找树是⼀个有序树
- 若它的左⼦树不空,则左⼦树上全部结点的值均⼩于它的根结点的值;
- 若它的右⼦树不空,则右⼦树上全部结点的值均⼤于它的根结点的值;
- 它的左、右⼦面试毛遂自荐简单大方树也分别为⼆叉排序树
平衡⼆叉查找树
平衡⼆叉查找树:⼜被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是⼀棵空树或它的左右两个⼦树的面试问题大全及答案大全⾼度差的绝对值不逾越1,并且左右两个⼦树都是⼀棵平衡⼆叉树。
堆
堆是一棵次序存储的彻底二叉树,堆的存数据结构储能够用数组来完结
-
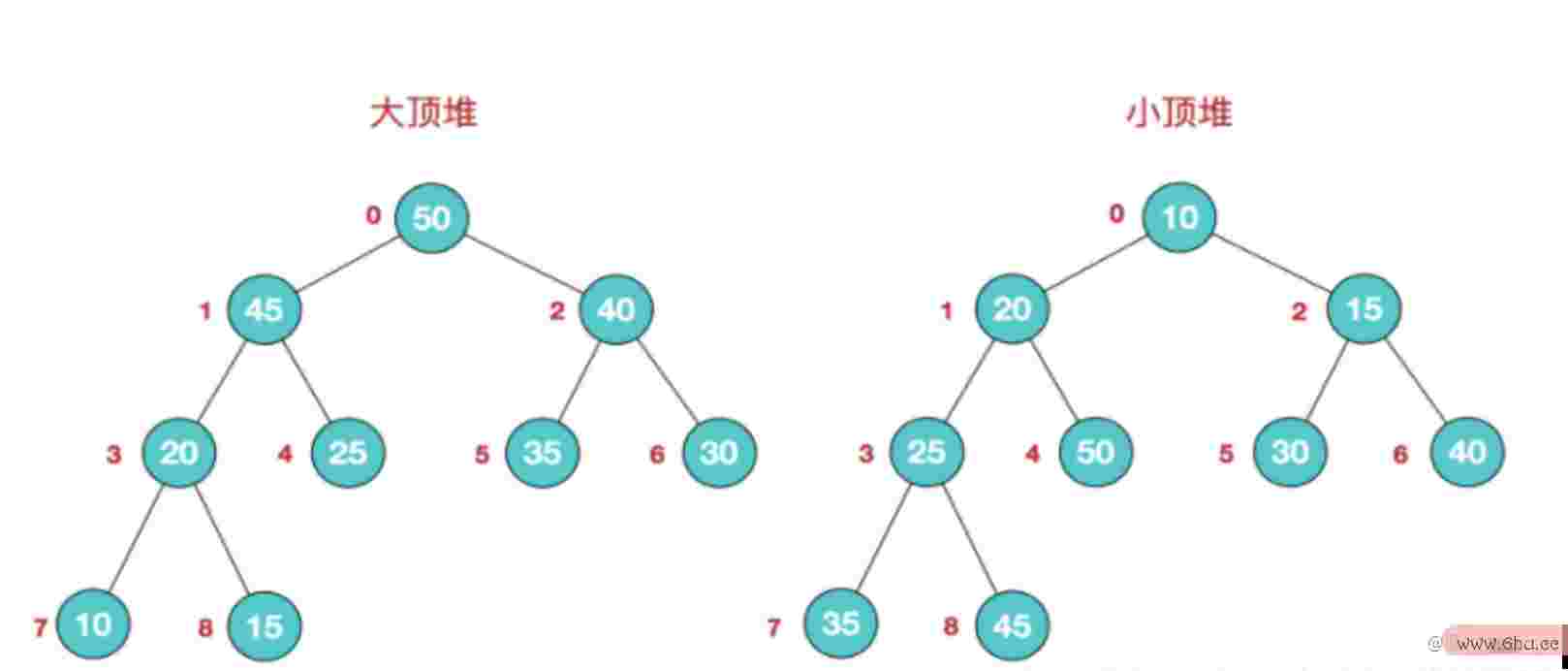
大顶堆复杂度o(1)什么意思: 每个结点的值都大于或等于其左右孩子结点的值
-
小顶堆: 每个结点的值都小于或等于其左右孩子结点的值复杂度o(1)什么意思
对于n个元素的序列{R0, R1, … , Rn}当且仅当满足下列联络之一时,称之为堆:
- Ri<= R2i算法剖析的意图是+1且Ri<= R2i+2(小顶堆)
- Ri >= R2i+1 且 Ri >= R2i+2 (大顶堆)
留意 : 没有要求结点的左孩子的值和右孩子的值的大小联络。
堆是特别的彻底二叉树,所以构造堆的进程是按算法剖析的意图是次序进行的,是从上至下,从左至右的次序. 堆的存储一般用数组来完结。假定堆数组的某个节点在数组中的下标为i,那么它的父节点下标为(i-1)/2;它的左子节点的下标为2*i+1;它的右子节点的下标为2*i+2。
大顶堆和小顶堆的示例
堆的运用—堆排序
升序排序用大算法导论顶堆,降序排复杂度剖析序用小顶堆
⼆叉树的存储办法
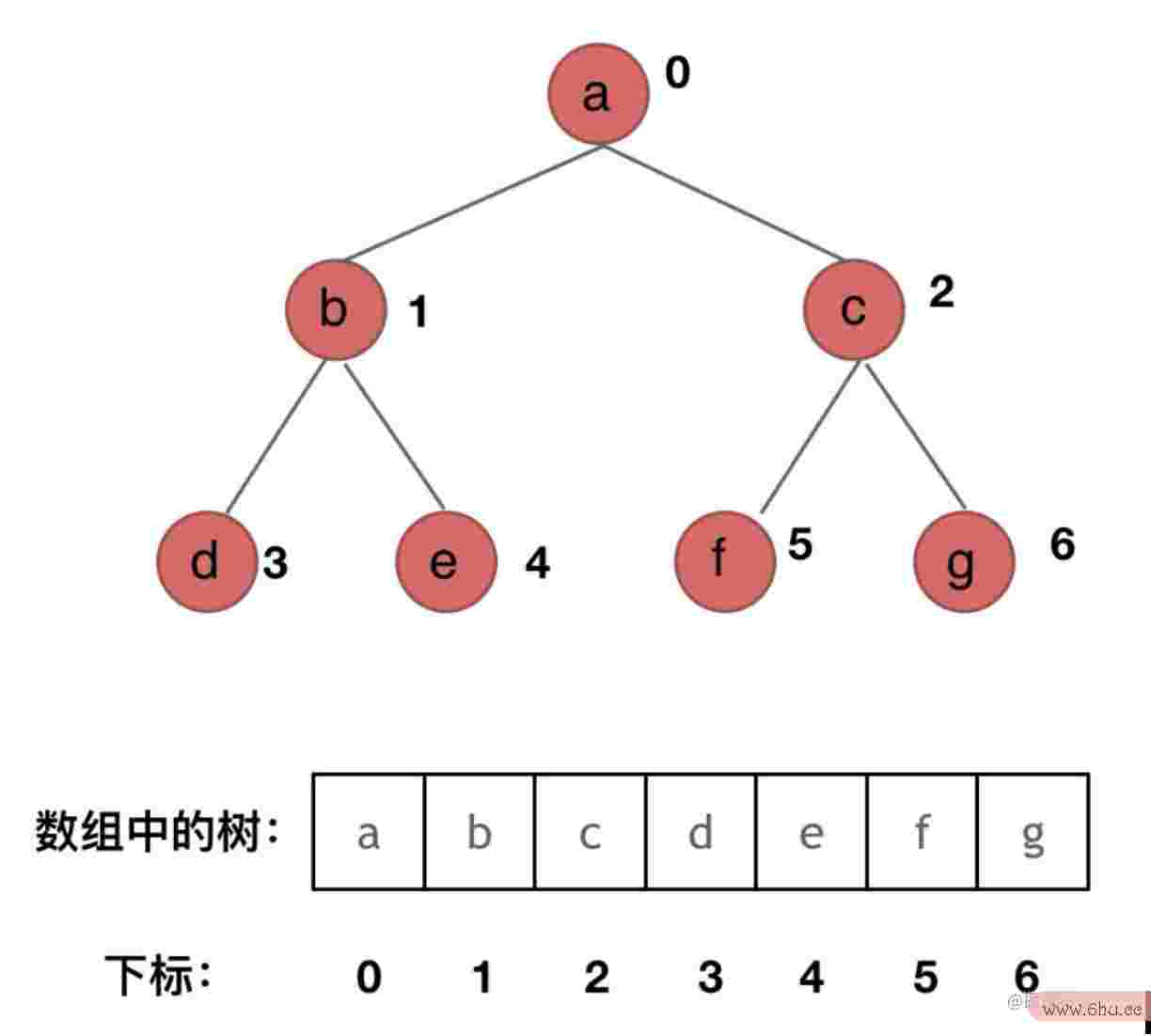
⼆叉树能够链式存储,也能够次序存储。链式存储用指针完结,⼆叉树的界说和链表很类似,⼆叉树的节点有两个指针,指向左右孩⼦;次序存储用一维数组来标明,次序存储的方算法的有穷性是指法如图
假定二叉树的某个节点在数组中的下标为i,那么它的父节点下标为(i-1)/2;它的左子节点的下标为2*i+1;它的右子节点的下标为2*i+2。
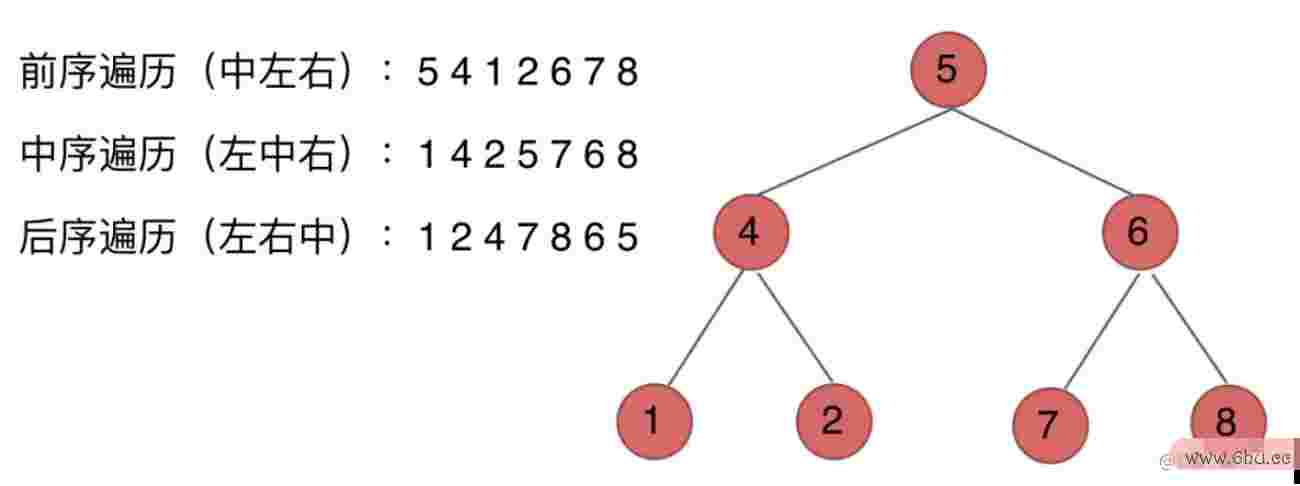
二叉树的遍历
二叉树的遍历办法有2种,深度优先查找(DF算法剖析的意图是S)和广度优先查找(BFS),深度优先查找又分为3种遍历办法:前中后序遍历,这三种遍历办法都能够用递归和迭代两种办法来完结。广度优先查找便是层次遍历,经过迭代来完结.
DFS的前中后序遍历的⾮递归的⽅式能够仰仗栈来完结;广度优先查找能够运用部队来完结,由于部队是先进先出的面试问题数据结构,只需先进先出才干保证一层层的遍历二叉树
重视我
假设觉得我写的不错,请点个赞 重视我 您的支撑是我更文最大的动力!



评论(0)