从零开始的数据结构Ep2-向量简介与分摊分析-六虎

零、前言

欢迎拜访：

个人主页：conqueror712.github.io/

Github主页：github.com/Conqueror71…

笔者注：

本文，乃至本系列是我用于辅佐自己学习的产品，难免会有些地方写的不如书本上那么准确，更多是关于常识结构的梳理以及自己的了解，毕竟不是要做一个“电子版的书本”，不会八面玲珑。不过也请感兴趣的读者们定心，省略掉的重要内容，文中都会有标识，如今无论是搜索引擎仍是语言模型，想必都能够很快地解决疑惑，感兴趣的话能够自行查找。

其他，我会将我自己梳理的常识结构图附上，以便咱们能愈加一目了然地了解常识点之间存在的联络，在这其间或许会有一些了解不到位，或许错误的内容，烦请咱们指出，这样一来也能更好地帮助其他有需求的人。关于每章节的课后习题，我计划在有需求的时分做成视频解说放在 Bilibili 上，供有需求的读者朋友们参考。

数据结构是数据项的结构化调集，而此处的结构性表现为数据项之间的彼此联络及效果，即数据项之间的某种逻辑次第。

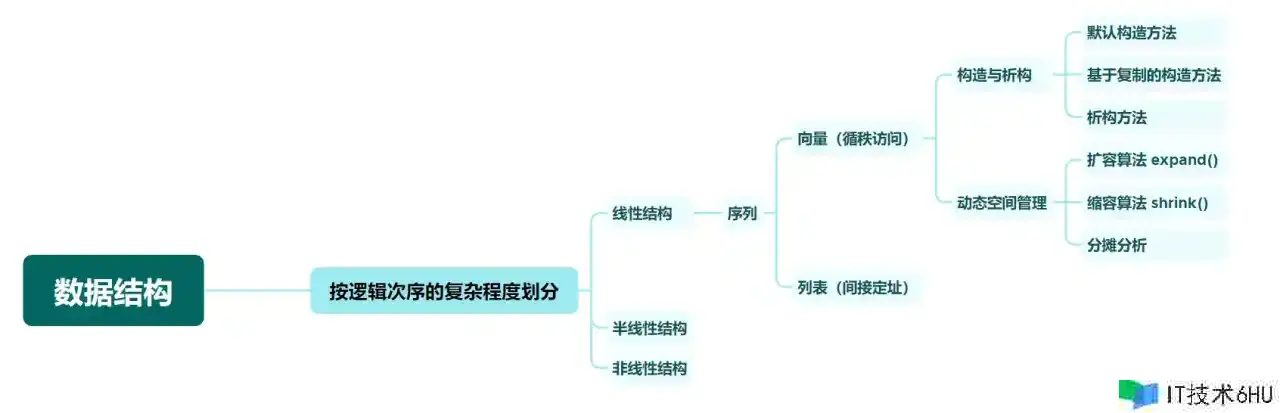
依照逻辑次第的复杂程度，能够将数据结构划分为三大类：

线性结构
半线性结构
非线性结构

在这里，咱们首先讨论线性结构的最基本方式——序列（sequence），而序列又能够依照其间寄存的数据项的逻辑地址与物理地址联络，分为两种：

向量（vector）：一切数据项的物理方位与其逻辑次第，即秩（rank），彻底吻合。
列表（list）：采用直接定址的办法，经过封装后的方位彼此引证。

一、数组与向量

数组（array）是一种很简单的线性结构，也能够作为向量的前身来看，即更特殊的向量。

关于数组而言，咱们需求知道以下几个名词的意义（内容比较基础，此处不做过多介绍）：

前驱（predecessor）
后继（successor）
直接前驱（immediate predecessor）
直接后继（immediate successor）
前缀（prefix）
后缀（suffix）

遗憾的是，一般来说，一个数组只能寄存同一类型的数据，假使咱们想要寄存多种类型的数据，这时分咱们就需求对其进行推广，得到所谓的向量，其间的元素分别由秩来彼此区别，彼此互异。经过秩 r，能够仅有确定 e = V[r]，这是向量特有的元素拜访办法，即循秩拜访（call-by-rank）。其实在这里，向量的秩和数组的下标起的效果差不多，咱们能够一起来了解。

其他，已然同一向量能够寄存不同类型的数据，那么就不能确保它们之间能够互相比较巨细。

二、Vector 模板类

typedef int Rank;	// 秩，或写成 using Rank = unsigned int;
#define DEFAULT_CAPACITY  3 // 默许的初始容量（实践运用中可设置为更大）
template <typename T> class Vector { // 向量模板类
protected:
	Rank _size; Rank _capacity;  T* _elem; // 规划、容量、数据区
	void copyFrom ( T const* A, Rank lo, Rank hi ); // 仿制数组区间A[lo, hi)
	void expand(); // 空间缺乏时扩容
	void shrink(); // 装填因子过小时压缩
	bool bubble ( Rank lo, Rank hi ); 			// 扫描交换
	void bubbleSort ( Rank lo, Rank hi ); 		// 起泡排序算法
	Rank maxItem ( Rank lo, Rank hi ); 			// 选取最大元素
	void selectionSort ( Rank lo, Rank hi ); 	// 挑选排序算法
	void merge ( Rank lo, Rank mi, Rank hi ); 	// 归并算法
	void mergeSort ( Rank lo, Rank hi ); 		// 归并排序算法
	void heapSort ( Rank lo, Rank hi ); 		// 堆排序（稍后结合彻底堆解说）
	Rank partition ( Rank lo, Rank hi ); 		// 轴点结构算法
	void quickSort ( Rank lo, Rank hi ); 		// 快速排序算法
	void shellSort ( Rank lo, Rank hi ); 		// 希尔排序算法
public:
// 结构函数
	Vector ( Rank c = DEFAULT_CAPACITY, Rank s = 0, T v = 0 ) // 容量为c、规划为s、一切元素初始为v
	{ _elem = new T[_capacity = c]; for ( _size = 0; _size < s; _elem[_size  ] = v ); } // s <= c
	Vector ( T const* A, Rank n ) { copyFrom ( A, 0, n ); } // 数组全体仿制
	Vector ( T const* A, Rank lo, Rank hi ) { copyFrom ( A, lo, hi ); } // 区间
	Vector ( Vector<T> const& V ) { copyFrom ( V._elem, 0, V._size ); } // 向量全体仿制
	Vector ( Vector<T> const& V, Rank lo, Rank hi ) { copyFrom ( V._elem, lo, hi ); } // 区间
// 析构函数
	~Vector() { delete [] _elem; } // 开释内部空间
// 只读拜访接口
	Rank size() const { return _size; } 	// 规划
	bool empty() const { return !_size; } 	// 判空
	Rank find ( T const& e ) const { return find ( e, 0, _size ); } // 无序向量全体查找
	Rank find ( T const& e, Rank lo, Rank hi ) const; // 无序向量区间查找
	Rank select( Rank k ) { return quickSelect( _elem, _size, k ); } // 从无序向量中找到第k大的元素
	Rank search( T const& e ) const // 有序向量全体查找
	{ return ( 0 >= _size ) ? -1 : search ( e, 0, _size ); }
	Rank search ( T const& e, Rank lo, Rank hi ) const; // 有序向量区间查找
// 可写拜访接口
	T& operator[] ( Rank r ); // 重载下标操作符，能够类似于数组方式引证各元素
	const T& operator[] ( Rank r ) const; // 仅限于做右值的重载版本
	Vector<T> & operator= ( Vector<T> const& ); // 重载赋值操作符，以便直接克隆向量
	T remove ( Rank r ); // 删除秩为r的元素
	Rank remove ( Rank lo, Rank hi ); // 删除秩在区间[lo, hi)之内的元素
	Rank insert ( Rank r, T const& e ); // 刺进元素
	Rank insert ( T const& e ) { return insert ( _size, e ); } // 默许作为末元素刺进
	void sort ( Rank lo, Rank hi ); // 对[lo, hi)排序
	void sort() { sort ( 0, _size ); } // 全体排序
	void unsort ( Rank lo, Rank hi ); // 对[lo, hi)置乱
	void unsort() { unsort ( 0, _size ); } // 全体置乱
	Rank dedup(); // 无序去重
	Rank uniquify(); // 有序去重
// 遍历
	void traverse ( void (* ) ( T& ) ); // 遍历（运用函数指针，只读或部分性修正）
	template <typename VST> void traverse ( VST& ); // 遍历（运用函数目标，可全局性修正）
};

这样，咱们就能够用 Vector<int>, Vector<float>, Vector<Vector<char>> 之类的方式了。

在代码的第 6 行，即 Rank _size; Rank _capacity; T* _elem; // 规划、容量、数据区，咱们在 Vector 的内部维护一个元素类型为 T 的私有数组 _elem[]，其容量由 _capacity 指定，其效果是存储向量的元素，这也是为什么咱们称之为数据区的原因。而向量当时的实践规划，即有用元素的数量则是由 _size 指定。

其他，补充一条关于内部数组 _elem[] 的阐明：V[r] 对应 _elem[r]，其物理地址为 _elem r。

三、结构与析构

向量目标的结构与析构，主要围绕上述私有变量和数据区的初始化与销毁打开，咱们有两种常用的结构办法（默许结构办法、依据仿制的结构办法）以及一种析构办法。

默许结构办法：

与一切目标相同，向量在运用前也需求先被体系创立，即凭借**结构函数（constructor）**来初始化。

因为向量是一种动态数据结构，其内部存储空间的管理需求在运用之前进行合适的初始化，所以需求运用结构函数来初始化，以确保向量在被创立后具有合适的内部状态，包含容量、规划和元素值等。

结构函数是一种特殊的成员函数，其用处便是如上文所述——在目标创立时对其进行初始化。其称号与类名相同，没有回来类型（void 也没有）。

结构函数在目标创立时主动调用，用于完结目标的初始化工作。关于向量来说，结构函数创立一个新的向量目标，并初始化其内部的元素数组、容量和规划等特点，使得向量目标能够被正确地运用。

进程如下：（花费常数时刻）
1. 依据指定的初始容量，向体系请求空间，以创立内部私有数组 elem[]，若不指定则运用 DEFAULT_CAPACITY
2. 因为初生向量（笑）还没有元素，所以用于指示规划的变量 _size 被初始化为 0

依据仿制的结构办法：

简单来说，便是以某个已有的向量（包含数组）作为蓝本，进行（部分 or 全体）仿制，以下给出一致的 copyFrom()：

template <typename T>	// 元素类型
// 以数组区间A[lo, hi)为蓝本仿制
void Vector<T>::copyFrom (T const* A, Rank lo, Rank hi){ 
    // 分配空间，规划清零
    _elem = new T[_capacity = 2 * (hi - lo)];
    _size = 0;
    while (lo < hi){	// 逐一仿制
        _elem[_size  ] = A[lo  ];
    }
}
// 因为向量内部含有动态分配的空间，默许的"="运算符缺乏以支持赋值，所以需求重载：
template <typename T> Vector<T>& Vector<T>::operator = (Vector<T> const& V){
    if (_elem){
        delete [] _elem; // 开释原有内容
    }
    copyFrom(V.elem, 0, V.size()); // 全体仿制
    return *this; // 回来当时目标的引证，以便链式赋值
}

析构办法：

与一切目标相同，不再需求的向量应该凭借析构函数（destructor）及时整理，毕竟体系资源很宝贵。与结构函数不同，同一目标只能有一个析构函数，不能重载。

进程如下：（花费 O(1) 时刻）
1. 开释用于寄存元素的内部数组 _elem[]，将其占用的空间交还给 OS
2. 其余内部变量无需处理，将作为向量目标本身的一部分被体系回收
需求阐明的是，如果需求析构的内容包含动态分配的空间，因为这里没有重载，所以依照“谁请求谁开释”的原则来进行预处理（先于析构进行），至于要开释仍是保留，由上层调用者来决议。

四、动态空间管理、分摊剖析

运用结构函数创立的 Vector 目标有自己的初始容量，但假使容量一直固定，难免会遇到上溢（overflow）的状况，即装填因子（load factor）大于 1 了（ $装填因子=_size/_capacity$ ）。

此刻，运用可扩大向量就能够有用防止这种问题，其扩大战略是这样的：当原有数组满了的时分，会请求一个新的且容量更大的数组，并把原有数组的内容仿制曩昔，最终开释原有数组，这样能够确保数组内部空间的接连性。咱们能够用如下代码来表示这种 expand() 扩容算法：

template <typename T> void Vector<T>::expand(){
    if (_size < _capacity){
        return;
    }
	if (_capacity < DEFAULT_CAPACITY){	// 确保不低于最小容量
        _capacity = DEFAULT_CAPACITY;
    }
    T* oldElem = _elem;
    _elem = new T[_capacity <<= 1];	// 常见的是容量加倍，当然也能够是其他倍数
    for (int i = 0; i < _size; i  ){
        _elem[i] = oldElem[i];	// 仿制
    }
    delete [] oldElem;	// 开释
}

与之相对的，当装填因子小于某一阈值的时分，数组或许会发生下溢（underflow），这虽然是个不太常见的名词，但是如果说“发生糟蹋”就很好了解了，这在有些注重空间利用率的场合里面仍是很重要的，为此，咱们给出与 expand() 扩容算法类似的 shrink() 缩容算法，思路是相同的，就不过多赘述：

template <typename T> void Vector<T>::shrink(){
    if (_capacity < DEFAULT_CAPACITY << 1){	// 防止收缩到默许值以下
        return;
    }
    if (_size << 2 > _capacity){	// 以25%为阈值
        return;
    }
	T* oldElem = _elem;
    _elem = new T[_capacity >>= 1];	// 常见的是容量减半
    for (int i = 0; i < _size; i  ){
        _elem[i] = oldElem[i];	// 仿制
    }
    delete [] oldElem;	// 开释
}

在动态空间管理的进程中，分摊剖析是确保运转功率的一个重要工作。

分摊运转时刻（amortized running time）：

假设对可扩大向量进行满足多次接连操作，并将期间消耗的时刻分摊至一切的操作，如此一来得到的单次操作的平均时刻成本便是分摊运转时刻。

这里先直接给出一个定论：单次扩容或缩容所需的分摊运转时刻是 O(1) 的，证明进程请见文末习题。
平均运转时刻（average running time），也称希望运转时刻：

依照某种假定的概率散布，对各种状况下所需求的执行时刻的加权平均。

✍️相关练习解说视频（行将上线）

Question: 对 expand() 扩容算法进行分摊剖析。

// 代码重现
template <typename T> void Vector<T>::expand(){
    if (_size < _capacity){
        return;
    }
	if (_capacity < DEFAULT_CAPACITY){	// 确保不低于最小容量
        _capacity = DEFAULT_CAPACITY;
    }
    T* oldElem = _elem;
    _elem = new T[_capacity <<= 1];	// 常见的是容量加倍，当然也能够是其他倍数
    for (int i = 0; i < _size; i  ){
        _elem[i] = oldElem[i];	// 仿制
    }
    delete [] oldElem;	// 开释
}

解：

调查最坏状况——接连 $n$ 次扩大操作， $n \to \infty$ ，设数组的初始容量为常数 $N, (n >> N)$

欲估量复杂度上界，不妨设向量的初始规划 = 初始容量 = $N$ ，也便是行将溢出的状况

界说如下函数：

size(n) = 接连刺进n个元素后的向量规划
capacity(n) = 接连刺进n个元素后的数组容量
time(n) = 为了接连刺进n个元素，而花费在扩容上的时刻

易得 $s i ze (n) = N n$

由算法特点，得 $50% \leq 装填因子 \leq 100%$ ，即 $50%≤size(i)capacity(i)≤100%50% ≤ frac{size(i)}{capacity(i)} ≤ 100%$

∴有 $s i ze (n) \leq c a p a c i t y (i) \leq 2 s i ze (n)$ ，满足 $c_1h(n) ≤ T(n) ≤ c_2h(n)$ ，即大记号界说

又∵ $N$ 是常数，所以由 $T (n) = (h (n))$ 得 $c a p a c i t y (n) = (s i ze (n)) = (n N) = (n)$

∵ $n$ 的增长速度是 $2×2^x$ ，即 $2, 4, 8, 16\dots$

∴容量的增长速度也是 $2×2^x$ ，故在容量达到 $c a p a c i t y (n)$ 之前，会做 $log_2n)$ 次扩容

又∵每次扩容的时刻开支 $\propto$ 当时的规划（也便是容量，因为那时分持平）

∴ $t im e (n) = 2 N 4 N 8 N 16 N \dots c a p a c i t y (n) \leq 2 c a p a c i t y (n) = (n)$ ，（该放缩可用等比数列求和公式得到）

∴分摊到每次操作上需求的时刻开支便是 $(n)n=(1)frac{(n)}{n}=(1)$

从零开始的数据结构Ep2-向量简介与分摊分析

零、前言

一、数组与向量

二、Vector 模板类

三、结构与析构

四、动态空间管理、分摊剖析

相关文章

PaddleDetection目标检测套件

Compose 为什么可以跨平台？

你真的了解 Java 多态吗？深入浅出地探究多态的实现和应用

极智AI | opencv 你真的会用吗？

作者信息