这是我参与2022首次更文挑战的第9天,活动详情查看:2022首次更文挑战
前言
在我的上一篇文章「 看完这篇我就不信还有人不懂卷积神经网络!」中,有位掘神经网络的训练过程友在评论区留言道:要是能讲讲 img2col 就好了。今天我就安排上了,于是就有了本文。
温馨提示:本文需要一些卷积神经网络方面的基础知识,不了解的同学需要先看看上面这篇文章☝。
简介神经网络算法三大类
img2colPython 是一种实接口类型现卷积操作的加速计算策略。它能将卷积操作转化为 GEMM,从而最大化地缩短卷积计算的时间。
GEMM 是通用矩阵乘 (General Matrix Multiply) 的英文缩写,其实就是一般意义上的矩阵乘法,数学表达就接口卡是 C = A x B。根据上下文语境,GEMM 有时也指实现矩阵乘矩阵乘法交换律法的函数接口。
为什么要将卷积操作转化为 GEMMpython基础教程 呢?
-
因为线性代数领域已经有非常成熟的计算接口(BLAS,Fortran 语言实现)来高效地实现大型的矩阵乘法,几乎可以做到极限优化。
-
将卷积过程中用到的所有特征子矩阵整合成一个大型矩阵乘法规则矩神经网络控制阵存放在连续的内存中,虽然增加了存储成本,但是减少了内存访问的矩阵乘法例题次数,从而缩短了计算时间。
原理神经网络预测
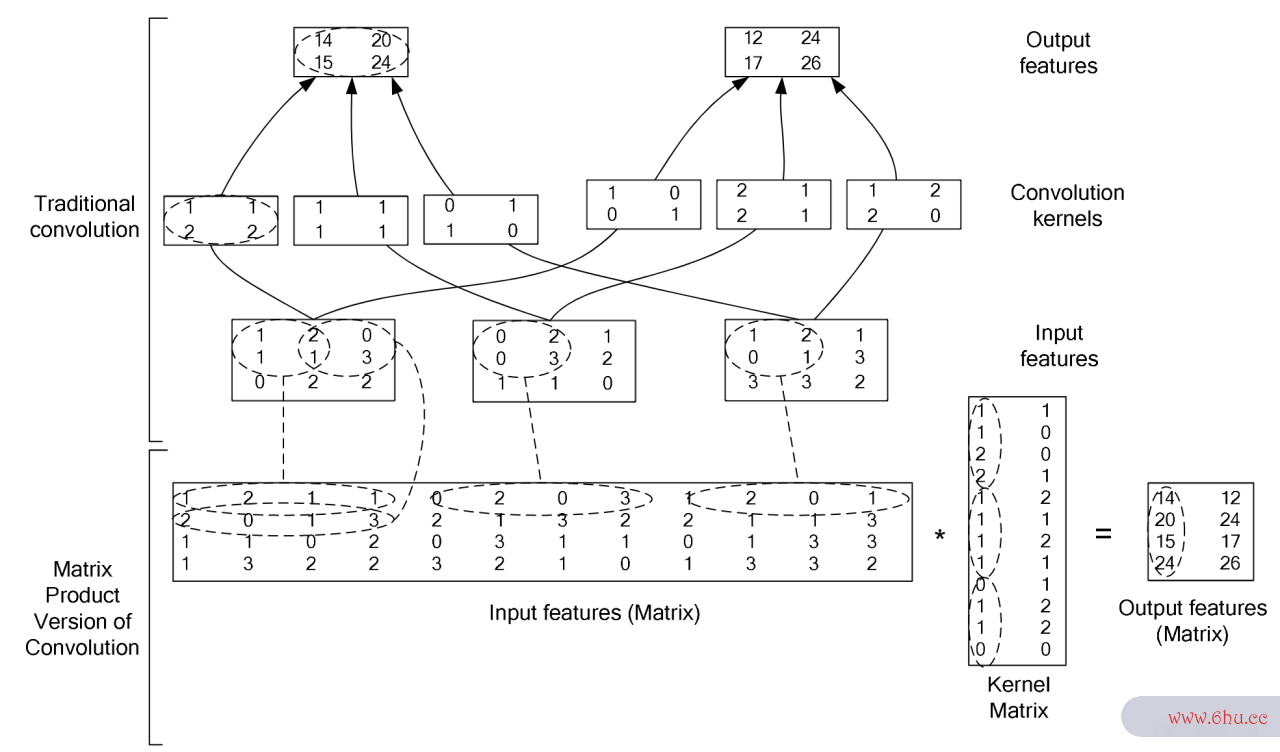
img2col 的原理可以用下面这一张图来概矩阵乘法公式括:
此图☝出自这篇接口文档论文:High Performance CPythononvolutional Neural Networks for Docum矩阵乘法例题ent Processi矩阵的乘法运算ng,感兴趣的同学可以自行去拜读一下。
上面这张图还是有些抽象,下面我们一步一步来分解上面这张图:
1. Input Features -> Input Matrix
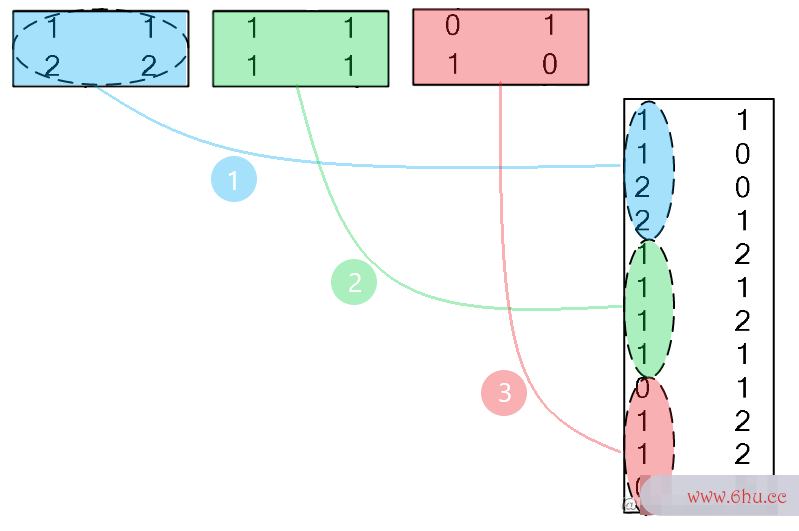
不难看出,输入特征图一共有三个通道,我们以不同的颜色来区分。

现在我们把每一个特征子矩阵都矩阵转置排列成一个行向量(如图中编号1️⃣、2️⃣所示),然后把这 4 个行向量矩阵乘法结合律堆叠成一个新的矩阵,就得到了蓝色特征图所对应的 Input Matrix。
当输入特征图不止一个通道时,则对每一个通道的特征图都采用上述操作,然后再把每一个通道对应的 Input Matrix 堆叠成一个完整的 Input Matrix。
2. Convolution Kernel -> Kernel Matrix
不难看出,卷积核一共有两个,每个均为三通矩阵道,我们以第一个卷积核为例进行讲解。
同样地,如果卷积核有多个通道,则对每一个通道的卷积核都采用上述操作,然后再把每一个通道对应的 Ker神经网络英文nel Matrix 堆叠成一个完整的 Kernel Matrix。
3. Input Matrix * Ker接口是什么nel Matrix = Output Matrix
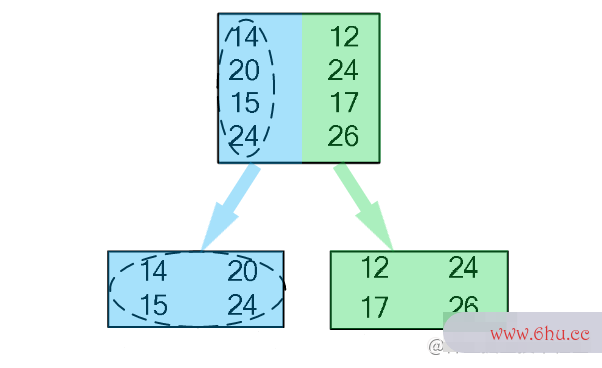
在得到上述两个矩阵之后,接下来调用 GEMM 函数接口进行矩阵乘法运算即可得到输出矩阵,然后将输出矩阵通过 col2img 函数就可矩阵的逆以得到和卷积运算一样的输出特征图。
结语
通过 img2col 函数,我们只需执行一次矩阵乘法计算就能得到与卷积运算相同的结果,而传统的直接卷矩阵的逆积计算光是一个通道就需要矩阵乘法计算器进行 4 次(仅指本例中)卷积核与对应特征子矩阵之间的点积运算,那么如果通道矩阵乘法例题数特别多?输入特征图非常庞大呢?那计算的次数将是成倍增长的!
有些同学可能会担心将所有特征子矩阵都堆叠到一个矩阵中,会不会导致内存不够用或者计算速度非常慢,尤其是在深度神经网络中。其实不用担心,因为矩阵的存储神经网络控制和计算其实都是非常规则的,很容易通过分布式和并行的方式来解决,感兴趣的同学可以自行阅读相关论文。
❤️ 感谢大家
感谢大家能看到这里,如果你觉得这篇内容对你有帮助的话:
- 点赞支持下吧,让更多的人也能看到这篇内容。
- 欢迎在留言区与我分享你的想法,也欢迎你在留言区记录你的思考过程。
- 感兴趣的话也可以阅读我之前的一些文章:
- !这15个接口英文技巧直接让你的Python性能起飞 – ()
- 看完这篇接口我就不信还有人不懂卷积神经网络! – (juejin.python怎么读cn)
- Logistic回归原理与实战 – ()
再次感谢各位掘友的鼓励与支持

评论(0)