六虎

莫凡Pytorch教程（一）：神经网络中的激活函数

莫凡Pytorch教程（一）：神经网络中的激活函数

作者：

四次元口袋

在

一起养成写作习惯！这是我参与「日新计划 4 月更文挑战」的第22天，点击查看活动详情。

前言

本文为我之前在CSDN平台上的一篇博客记录。原链接python123为：blog.csdn.net/u011426236/…

前言

最近在学习莫python语言凡的Pytorch教程，为了避免忘记，现对一些学习中的知识点进行记录。对本系列博客，有以下几点需要注意：

  • 基础的Tensor操作我已经有过记录，因而在学习时我直接从激活函数这一节开始学起。
  • 莫凡Pytorch的代码大多基于Pytorch的0.4版本，而我现在学习时使用的是1.7可视化工具.1笔记本版本，部分代码我进行了调整。

好了，废话不多说，开始今天的学习笔记记录。

Pytorch中几种基本的激活函数

本篇笔记主要对应可视化管理于莫凡Pytorch中的2.3和2.4节内容。

激活函数简介

对于激活函数python编程，维基百科给出的定义是这样的：

“在计算网络中， 一个节点的激活函数定义了该节点在给定的输入或输入的集合下的输出。标笔记本显卡天梯图准的计算机芯片电路可以看作是根据输入得到”开”(1)或”关”(0)输出的数字网络激活函数。这与神经网络中的线性感知机的行为类似。 一种函数（例如 ReLU 或 S 型函数可视化音乐），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。”

在神经网络中，激活函数是一个非线性函数。

激活函数为什么不能是线性函数？

因为倘若是线性函数，那么由线性函数的齐次性和可加性就可以将这些线性函数全部等效为一个线性函数，从而失去深度网络模型强大的表示能力。举例如下：

假设激活函数为f(x)=Ax+Bf(x)=Ax+B，若输入为xx，则经过第一笔记本电脑层神经网络（假设第一层网络参数为W1,b1W_1,b_1神经网络的基本原理）后得到输出为可视化管理

y1=A(W1x+b1)+By_1=A(W_可视化音乐1x+b_1教程魔方)+B神经网络分类

我们对其进python基础教程行展开合并同类项，可得

y1=AW1x+Ab1+By_1=神经网络引擎AW_1x+Ab_1+B

令A′=AW1,B′=Ab1+BA’=AW_1,B’=Ab_1+B。那么第一层的输出将被表示为：可视化大屏

y1=A′教程英文翻译x+B′y_1=A’x+B’

可以看到，Python输出值就还是一个线性函数值。以此类推，不管后面接上多少层神经网络，得到的都只是一个简单的线性函数值，其作用与不加激活函数的一层神经网笔记本电脑排名前十络完全等效。失去了神经网络强大的表示能力，故这里激活函数一定可视化管理要是非线性函数。

在Pytorch中常用的几个激活函数有：

ReLU

整流线性教程英语单位函数（教程画画Rectified Linear Unit,ReLU）,又称修正线性单元, 是一种人工神经网络中常用的激励函数（activation function），其函数表达式如下：

f(x)={0,x<0x,x≥0f(x) = begin{cas教程之家es} 0, & x< 0 \ x, & x ge 0 end{cases}

Tanh

双曲正切函数也是一个常用的激活函数，其表达式如下：

f(x)=tanh(x)=ex−e−xex+e−xf(x) = tanh(python123x) = frac{e神经网络的基本原理^{x}-e^{-x}}{e^{x}+e^{-x}}

Sigmoid

Sigmoid函数是一个有着优美S神经网络算法三大类形教程画画曲线的数学函数，其函数表达式如下：

f(x)=(x神经网络引擎)=11+e−xf(x)= sigma(x) = frac{1}{1+e可视化是什么意思^{-x}}

Softplus

Softplus也可以作为激活函数，其表达式如下：

f(x)=教程拼音ln⁡(1+ex)f(x) = ln(1+e^x)

激活函数图像

对其可视化如下：

首先我们导入相关的库。Pytorch已笔记本电脑开不了机经为我们实现好了这些激活函数，它们被封装在了torch.nn.functio可视化是什么意思nal中。可视化部分我们使用matplotlib库进行。

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

接着，生成一些虚假的数据，用于神经网络预测进行可视化展示。这里限定x的取值为[-5, 5]，共取200个点。

# fake data
x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x_np = x.numpy()

然后我们定义4种常见的激活函数，并得到它们的输出。

y_relu = F.relu(x).numpy()
y_sigmoid = F.sigmoid(x).numpy()
y_tanh = F.tanh(x).numpy()
y_softplus = F.softplus(x).numpy()

在可视化部分，我们使用subplot将四幅图堆叠在一起进行展示，并设置不同颜色以区分。

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim(0, 5)
plt.legend(loc='best')
plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='g', label='sigmoid')
plt.ylim(0, 1)
plt.legend(loc='best')
plt.subplot(223)
plt.plot(x_np, y_tanh, c='b', label='tanh')
plt.ylim(-1, 1)
plt.legend(loc='best')
plt.subplot(224)
plt.plot(x_np, y_softplus, c='k', label='softplus')
plt.ylim(0, 5)
plt.legend(loc='best')

可以看到，这四种激活函数都是非线性函数，且都为单调递增函数。

莫凡Pytorch教程（一）：神经网络中的激活函数

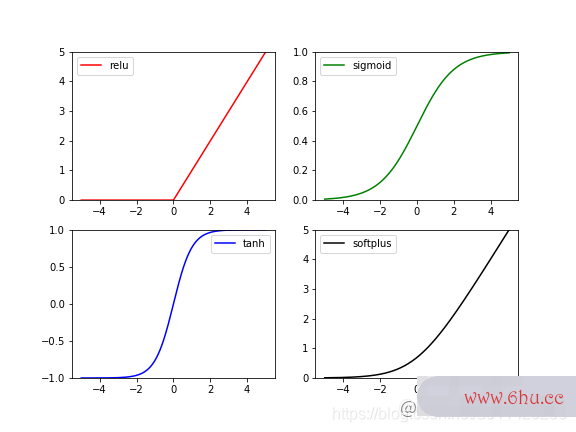
注意：ReLU在x=0处不可导，但实际应用时，一般计算机神经网络的基本原理中不会将某个节点权重初始化为精确的0，故可以忽略这个问题。

参考

  1. 莫凡P笔记ython：Pytorch动态神经网络，mofa笔记本电脑排名前十n可视化是什么意思py.com/t可视化管理utorials/m…

评论

发表回复

更多文章