LeetCode – #74 搜索二维矩阵

一起养成写作习惯！这是我参与「日新计划 4 月更文挑战」的第20天，点击查看活动详情。

前言

我们社区陆续会将顾毅（Netflix 增长黑客，《iOS 面试之道》作者，ACE 职业健身教swift是什么意思啊练。）的 Swift 算法题题解整理为文字版以方便大家学习与阅读。

LeetCode 算法到目前我们已面试常见问题及回答技巧经更新了 73 期，我们会保持更新时间和进度（周一、周三、周五早上 9:00 发布），每期的内容不多，我们希望大家可以在上班路上阅读，长久积累会有很大提升。

不积跬步，无以至千里；不积小流，无以成江海，Swift社区 伴你前行。如果复杂度怎么计算的大家有建议和意见欢迎在文末留言，我们会尽力满足大ios应用商店家的需求。

难度水平：中等

1. 描述圈复杂度

编写一个高效的算法Swift来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按swiftly升序排列。
• 每行的第一个整数大于前一行的iOS最后一个整数。

2. 示例

示例 1

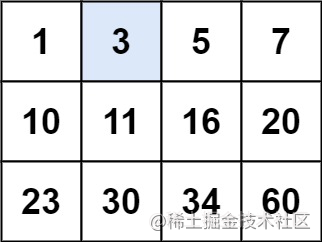
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2

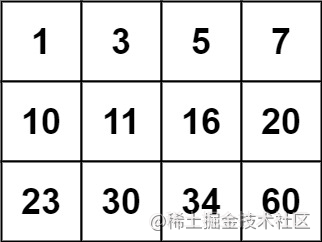
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

约束条件：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

3. 答案

class Search2DMatrix {
    func searchMatrix(_ matrix: [[Int]], _ target: Int) -> Bool {
        if matrix.count == 0 || matrix[0].count == 0 {
            return false
        }
        let rowNum = searchRow(matrix, target)
        return searchCol(matrix[rowNum], target)
    }
    private func searchRow(_ matrix: [[Int]], _ target: Int) -> Int {
        var left = 0, right = matrix.count - 1
        while left + 1 < right {
            let mid = (right - left) / 2 + left
            if matrix[mid][0] == target {
                return mid
            } else if matrix[mid][0] < target {
                left = mid
            } else {
                right = mid
            }
        }
        return matrix[right][0] <= target ? right : left
    }
    private func searchCol(_ nums: [Int], _ target: Int) -> Bool {
        var left = 0, right = nums.count - 1
        while left <= right {
            let mid = (right - left) / 2 + left
            if nums[mid] == target {
                return true
            } else if nums[mid] < target {
                left = mid + 1
            } else {
                right = mid - 1
            }
        }
        return false
    }
}

• 主要思想：搜索cswifterol，然后二分查找row。
• 时间复杂度： O(log(m + n))
• 空间复杂度： O环路复杂度(1)

该算法题解的仓库：LeetCode-Swift

点击前往 LeetCode 练习

关于我们ios越狱

我们是由 Swift 爱好者共同维护，我们会分享以 Swift 实战、SwiftUI、Swift 基础为核心的技术内容，也整理收集优秀的学习资料。