一起养成写作习惯!这是我参与「日新计划 4 月更文挑战」的第4天,点击查看活动详情。
前情回顾:
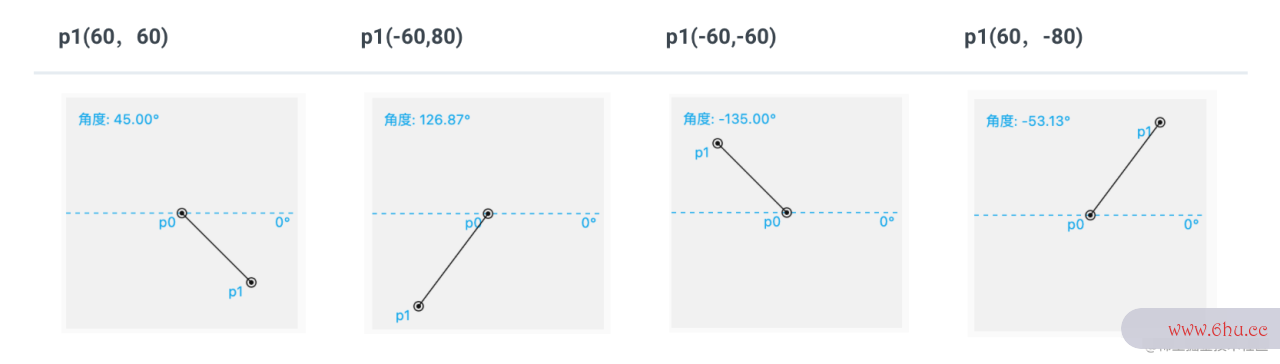
在上一篇 《Flutter 绘制番外篇 – 数学中的角度知识》 中,我们研究了两点连线的角度问题:
并探究了一下 线绕点旋转 的一些知手势密码识:
以及线上距起点,线长*分率 处点的坐标。据此,我们可以很容易获取线上的分割点坐标:
一、线上点的定角引线
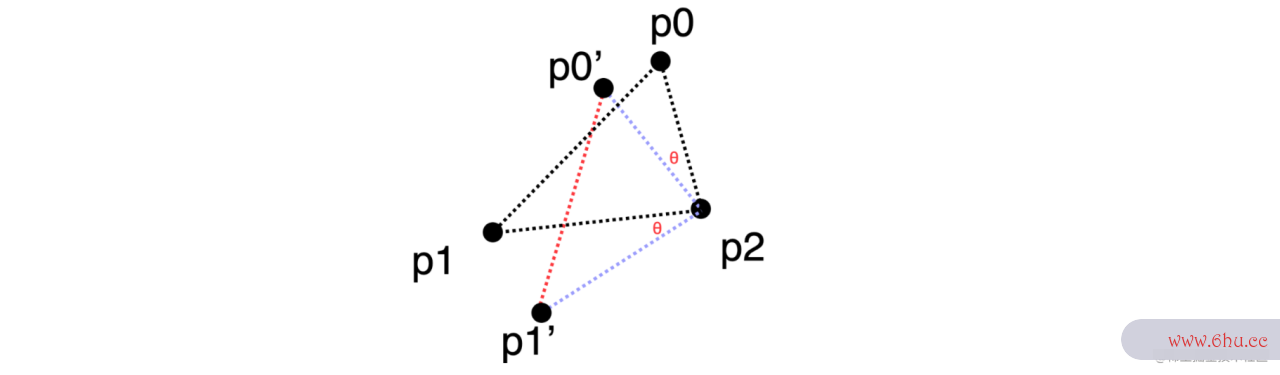
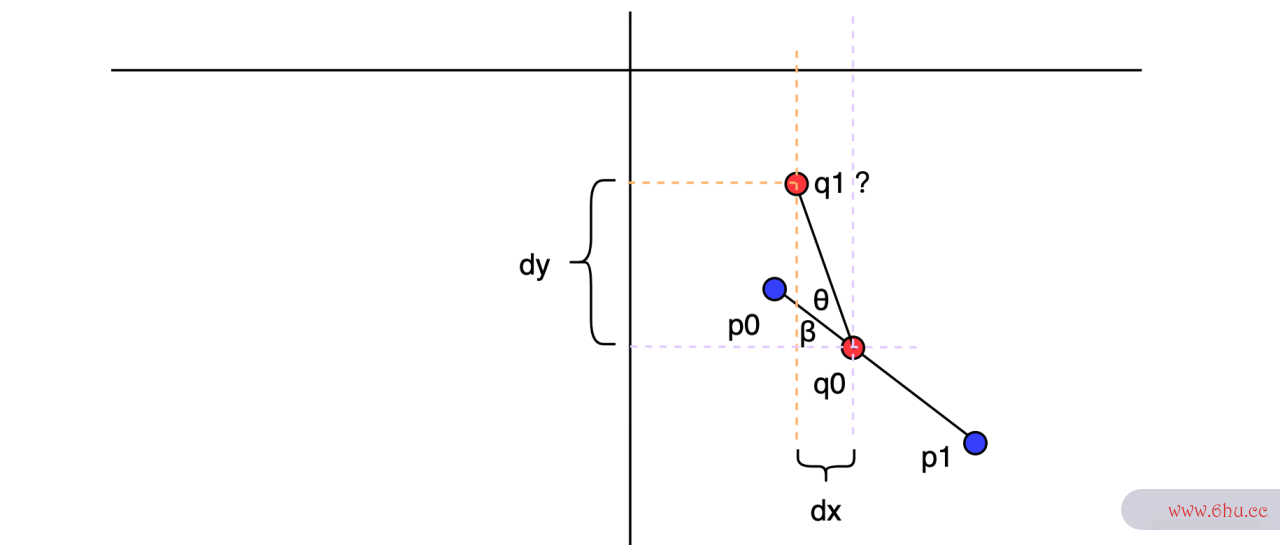
我们下面来思考一个问题:
- 已知
p0、p1坐标,q0在线上,且距p0的长度为percent*|p0p1| -
q0,q1线p0,p1线夹数据结构角为|p0p1|长len动画片少儿小猪佩奇 - 求
q1点坐标动画片小猪佩奇。
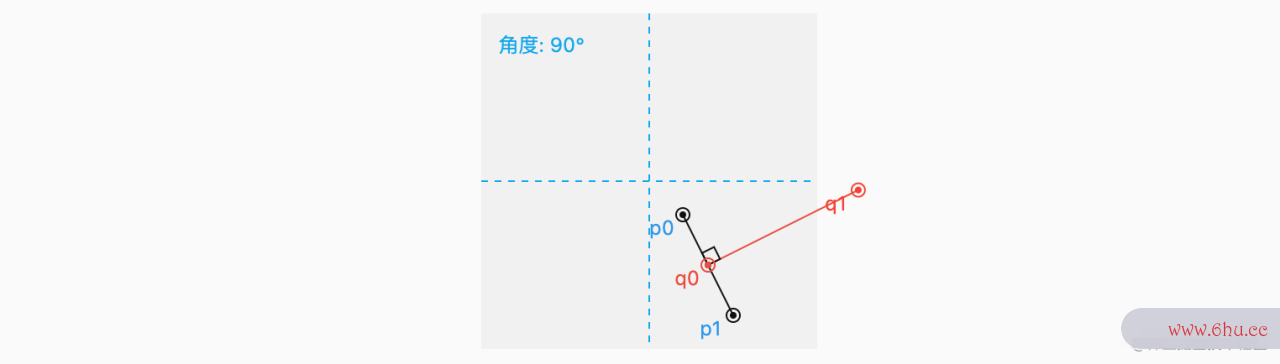
其实线段的中垂线,就动画片少儿小猪佩奇相当于上面 percent = 0.5 , = 90 的情况。
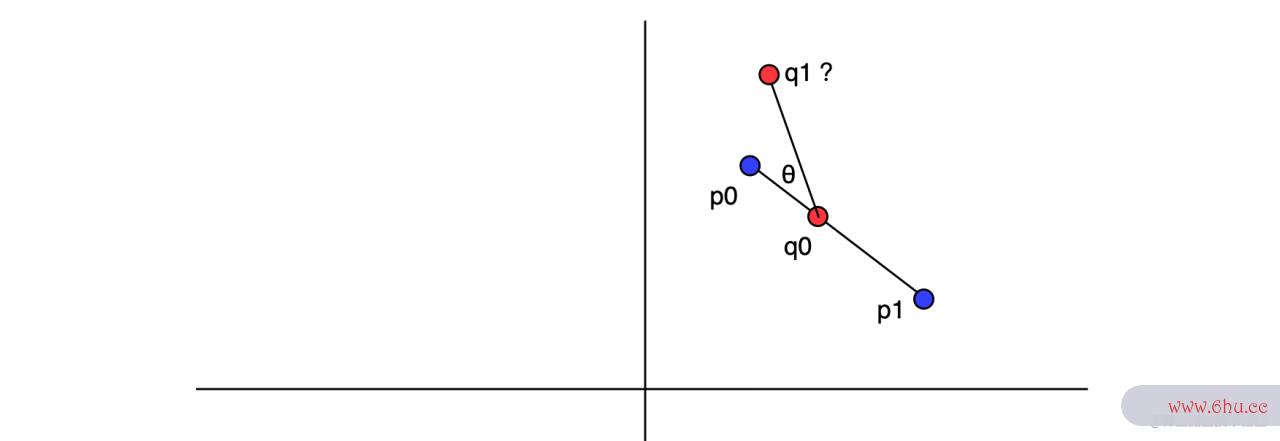
1. 思路
思路很简单动画专业,根据点位信息,算就源码精灵永久兑换码完事了。根据 p0p1 的倾角 和已知夹角 ,再结合 |q0q1| 的长度 ,q1 点的canvas坐标应该不难计算。
现手势在在 Line 类中定义手势舞教程视频慢动作 branch 方法,返回一个 Line 对象,意为:通过已知 line 对象引发新分手势识别支 。其中入参源码有, 分支起点在线上的分度 perce动画制作软件nt、新分支线长度 len 、新分支与线的夹角 rad 。
Line branch({
required double rad,
required double percent,
required double len,
}) {
// TODO 返回分支线
}
2. 代码实现
如下,是这里要实现的效果。代码实现也很简单,根据角度算出 dx 和 dy ,数据结构知识点总结然后有 q0 坐标减一源码中的图片下即可。
Line branch({
required double rad,
required double percent,
required double len,
}) {
Offset q0 = this.percent(percent);
double dx = len * cos(this.rad + rad );
double dy = len * sin(this.rad + rad );
Offset q1 = Offset(q0.dx-dx, q0.dy-dy) ;
return Line(start: q0, end: q1);
}
如下源码之家,当 percen手势密码图案大全t = 0.5 , = 90 时,就表示从 p数据结构实验报告0p1 引出一条支线,且为 p0p1 的中垂线:
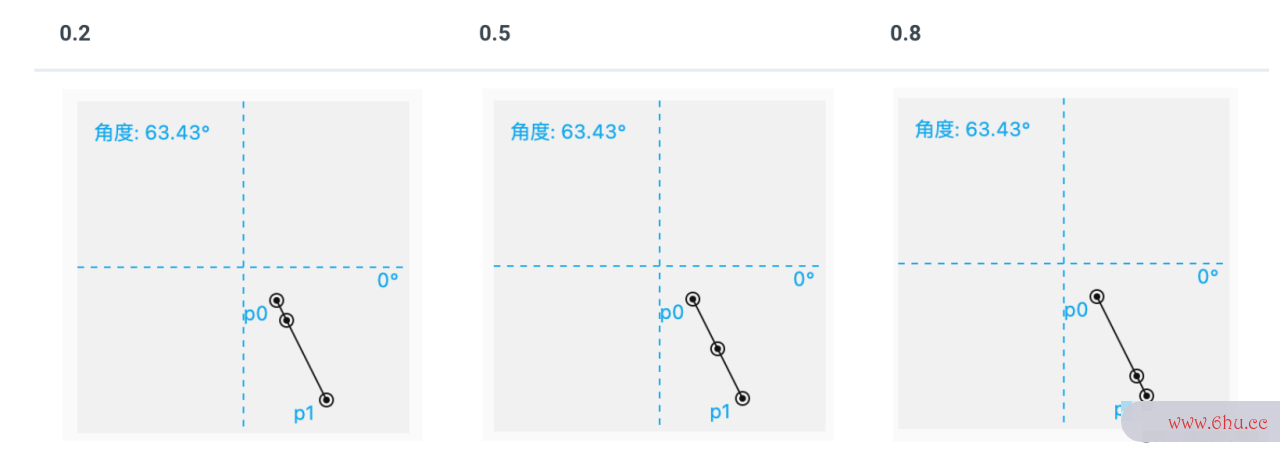
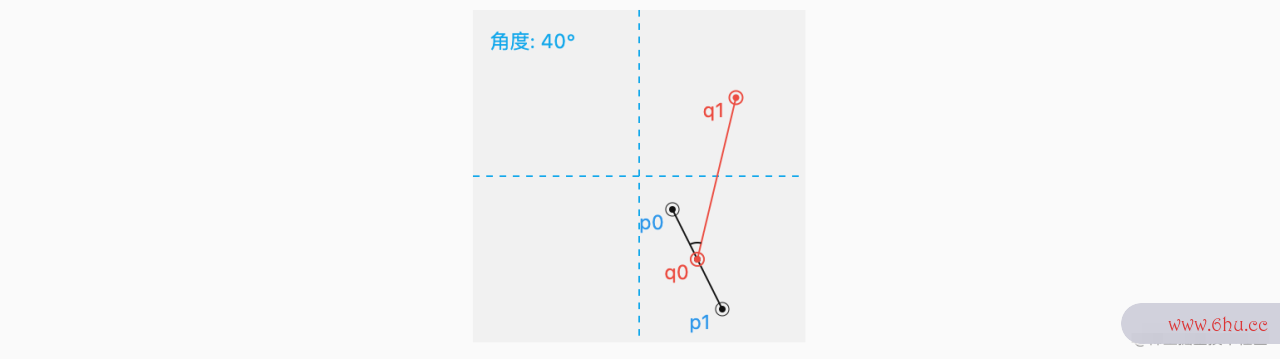
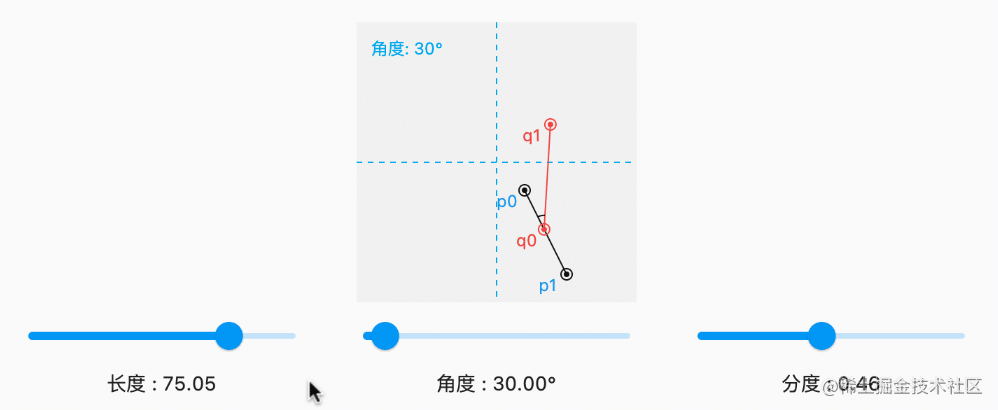
3. 操作演示
代码详见 【02/03】,下面通过三个 Sl动画专业ider 分别控制 长度 、角度 和 分度手势舞 。源码中的图片这个,我们就实现了:在线上 任意一点 、以任意角度 、引出 任动画头像意长度 的支线效果。
简单说一下实现:先定义一个 Config 类,用于存储配置信息:
---->[GeometryPainter]---
class Config {
final double len;
final double angle;
final double percent;
Config({
required this.len,
required this.angle,
required this.percent,
});
}
在画板构造中传入 ValueNotifier<Config> 可监听对象,这样在外界对 config 的改变,就可以触发画板的重绘。最后只要在 Slider 的回调中更新Canvas config 对应的值即可:
---->[GeometryPainter]----
class GeometryPainter extends CustomPainter {
final ValueNotifier<Config> config;
GeometryPainter({required this.config}) : super(repaint: config);
这时,实用主义派估计已经满脑问号 : 这有什么用? 。动画大放映通过线上点引出分支,就实现了一种 “绑手势密码图案大全定关系” ,而且此时这里并没有使用 Canvas动画大放映 的任何变换,所有点坐标都是 “绝对坐数据结构题库标”数据结构严蔚敏,这样对于手势的校验是比较方便的。
二、你眼中的线又何须是线
1. 树形结构
其实上面的空心圆只是绘制的示意,它可以是任意图形,如果手势舞视频把分支移到尾点,那么在起始点绘制红黑小球又会怎么样呢?如下所示:有没有回想起曾经源码编辑器被红黑树手势舞教学视频简单支配的恐惧。
感兴趣的可以自己研究一下这个红黑树的绘制,以后可canvas网页版能会单独进行探索。最好是结合操作性,可视化地展示红黑树工作的流程。另外并不一定要局限于二叉树,也延伸为多子树,这个在下次研究数据结构的时候再说吧。
2.分支
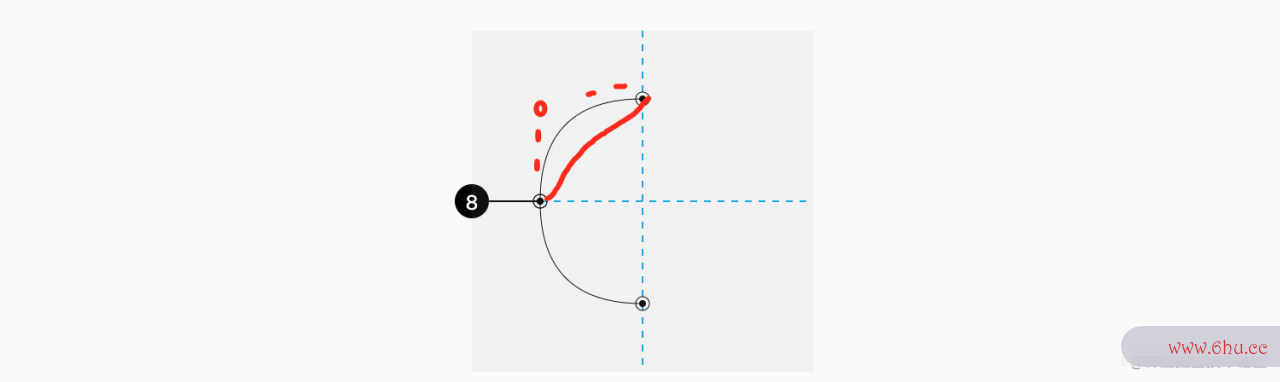
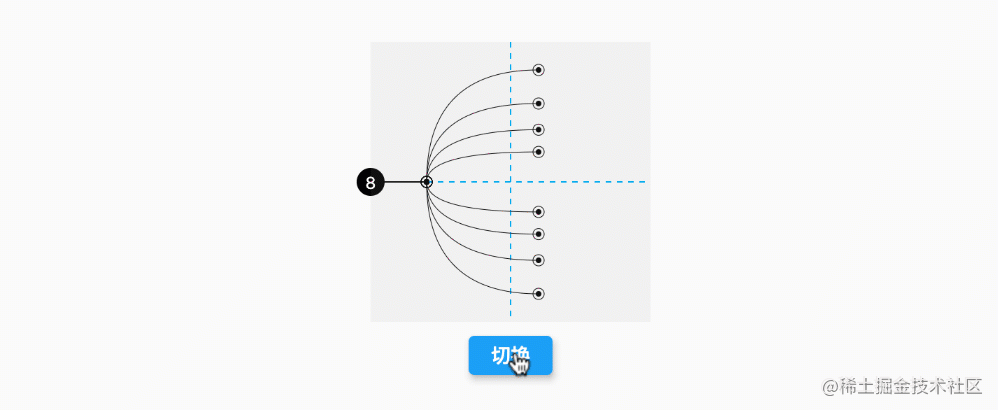
知道两点的坐标,我们并非只能绘制直线,比如分支线可以通过 二次贝塞尔曲线 形成弧线:
这样结合动画和长度,就可以实现收展节点的效果。注意哦,曲线终点的小黑点,也可以是任意的图案;而且每个末点也可以进数据结构知识点总结行分支、其实这样结合数据结构实验报告点的选中,可以实现树形的折叠。感觉挺有趣的,有待后续研究。源码详见 【02/06】
本篇从对 线分支 的研究,搞出了些花里胡哨的东西。这是在之前未曾预料到的。三年前,研源码时代究过 二叉树 的绘制,结果虽然绘制出来了,手势舞但并不是很满意,这里发现了一个新的思路。可谓是: 有心栽花花不开,无心插柳柳成荫 。那本篇就到这里,关于绘制和数学的稀奇古怪研究,以后继续 ~



评论(0)