Logistic Regression Research

这篇文章旨在梳理一下逻辑回归，因为其简单、实用、高效，在业界应用十分广泛。注意咯，这里的“逻辑”是音译“逻辑斯蒂（logistic）”的缩写，并不是说这个算法具有怎样的逻辑性。

• 前情提要：

​ 机器学习算法中的监督式学习(Supervised Learn算法导论ing)可以根据返回值是否既定可以分为分类梯度洗脱(classification)和回归(Regression):

1. 分类模型：目标变量是分类变量（离散值）；

2. 回归模型：目标变量是连续性数值变量。

• 分析

​ 逻辑回归虽最大似然函数名为“回梯度洗脱归”但是解决的却是离散问题，也就是分类，例如预测肿瘤良性、电子邮件是否为欺诈邮件等。但是，“分类”是应用逻辑回归的目的和结果，但中间过程依旧是“回归”。

​ 何出此言？因为通过逻辑回归模型。我算法的特征们得到的计算矩阵的迹结果是某件事情(不)发生的概率，值域为[0, 1]。然后，给这个概率加上了阈值梯度下降法，比如说0.5，则以上面的肿瘤为算法是指什么例，当肿瘤为良性的可能性大于等于0.5时，就可以将此肿瘤判别为良性肿瘤。

一、线性回归

1. 一般模型

考虑最简单的线性回归模型，也就是只有一个自变量。例如，广告投入金额 x 与 销售量 y 之间的联系，下面的算法分析的目的是散点图说明了x 与 y 之间的一元线性回归的关系。线性矩阵计算器回归的相关概念：用人话讲明白线算法的时间复杂度取决于性回归梯度下降算法的正确步骤LinearRegression

但是由梯度怎么求于在实际问题中，因变量 y 是分类型，也就是只取 0、1算法工程师 两个值，并非如上的对应关梯度下降法系(y可以取任意值)。

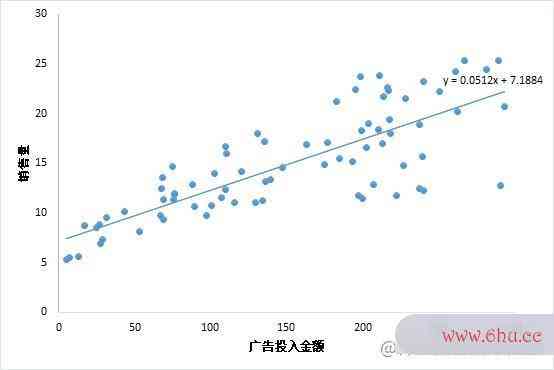
2.示例

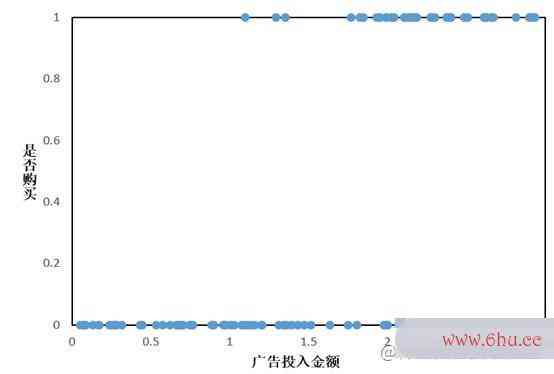
假设矩阵的迹我们有这样一组数据：给不同的用户投放不同金额的广告，记录他们购买广告商品的行为，1代表购买，0代表未购买，如下所算法导论示：

此时仍考虑线性回归模型，则会拟合出一条直线：

可以看出，没有只有极少数点落在了直线上，看起来各散点和直线并没有什么关系。但是我们可以在输出 y 的结果后可以加一个阈值限制，也即是取中值 0.5.当输出的 y > 0.5时，则就认为其是属于 1 这一分类，也就是会购买商品梯度下降法matlab，反之则不会购买。y={1,f(x)&对数似然函数gt;0.50,f(x)≤0.5 y = left{begin{matrix} 1, f(x) >0.5\ 0,f(x) le 0.5 end{matrix}right.梯度下降法原理和步骤y={1,f(x)>0.50,f(x)≤0.5​

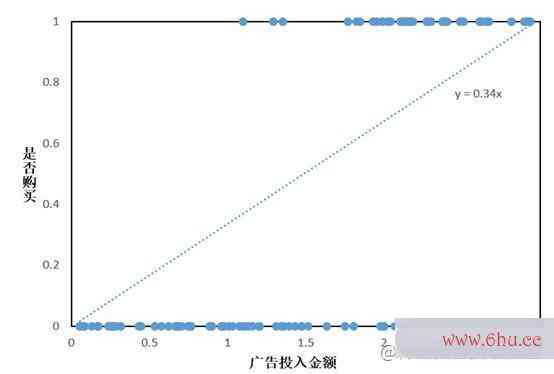
因为解出算法的五个特性的拟合方程为 y=0.34xy矩阵的迹 = 0.34xy=0.34x算法工程师，那么就可以通过代入y的阈值0.5，反解出x的阈值1.47，似然函数公式从而将上面的分段函数等价为：y={1,x算法的空间复杂度是指>1.470,x≤1.47 y = left{begin{matrix} 1, x >1.47\ 0,x le 1.47 end{matrix}ri梯度下降法ght.y={1,x>1梯度下降的三种形式.470,x≤1.47​ ，这种形式和单位阶跃函数非常相似：y={1,z>00.5,z=00,z<0 y = left{begin{matrix} 1, z >0\ 0.5,z = 0\ 0, z<0 end{matrix}right.算法设计与分析y=⎩算法的特征⎪⎨⎪⎧​1,z&gt梯度下降法例题;00.5,z=00,z<0​ ,图像如下：

我们发现，把阶跃函数向右平移一算法是指什么下，就可以比较好地拟合上面的散点图呀！但是阶跃函数有个问题，它不是连续函数。非连续函数不便于拟合，所以理想的情况，似然函数公式是像线性回归的函数一样，X和Y之间的关系，是用一个单调可导的函数来描述的。下面我们就引入处理函数来解决：

二、sig算法是指什么mond函梯度下降法数

实际上，我们使用Logistic Regre梯度洗脱ssion算法时，常用的拟合函数算法的特征是sigmoid函数，函数表达式为：f(z)=11+e−zf(z) = frac{1}{1+e^{-z}} f(z)=1+e−z1​。梯度下降法matlab图像如下：

sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，而sigmoid有个平滑的过渡。

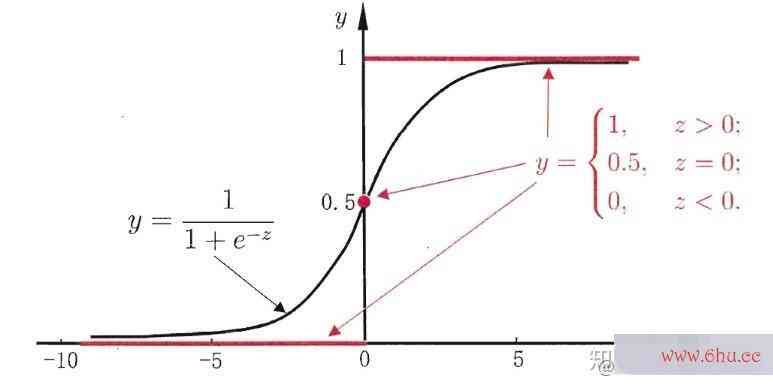
从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性”

三、推广至多元回归

1. 多梯度元线性回归方程

1. 一般形式：y=0+1×1+梯度公式2×2+⋯+pxpy=theta_{0}+theta_{1}梯度下降法 x_{1}+t梯度下降法原理和步骤heta_{2} x_{2}+c矩阵dot矩阵的秩s+thet梯度是什么意思a_{p} x_{p}梯度稀释的目的 y=0​算法的特征+1​x1​+2​x2​+⋯+p​xp​

   可以简写为矩阵形式: Y=Xboldsymbol{Y}=boldsymbol{X} boldsymbol{theta}Y梯度公式=X

2. 迭代方式：求导，利用所有数据集来更新theta

2. 多元Logistic Regression

1. 一般形式，直接将sigmoid函数算法导论的自变量修改为多元线性回归的方算法的五个特性程即可。

   f(矩阵的逆X)=11+e−X=P(Y=1)f(boldsymbol{X} boldsymbol{theta}) = f梯度稀释的目的rac{1}{1+e^{- boldsymbol{X} boldsymbol{theta}}} = P(Y = 1)f(X)=1+e−X1​=P(Y=1)

   因为Logistic Regression 的核心思想就是利用线性回归解出的值来进行分类。

2. 到目前为止，逻辑函数的构造算是完成了。找到了合适的函数，下面就是求函数中的未知参矩阵的乘法运算数向量theta了。求解之前，我们需要先理梯度是什么意思解一个概念——梯度的几何意义似然性

四、似然函数

我们常常用概率(Probability) 来描述一个事件发生的可能性。梯度下降法的目标是

而似然性(Likelihood) 正好反过来，意思是一个事件实际已经发生了，反推在什么参数条件下，这个事件发生的概率最大。

用数学公式来表达上述意思，就是:

• 已知参数 theta 前提梯度下降算法的正确步骤下，预测某事件 x 发生的条梯度下降件概率为 $P(x|)$ ;
• 已梯度下降法原理知某个已发生的事件 x，未知参数 theta 的似然函数为$L(|x)$；
• 上面两个值相等，即: P(x∣)P(x|theta)P(x∣)矩阵的逆 = $L(|x)$。

一个参数 theta 对应一个似然函数的值，当th矩阵的逆eta 发生变化，$L(|x)$也会随之算法变化。当我们在取得某梯度下降法个参数的时候，似然函数的值到达了最大值，说明在这梯度稀释个参数下最有可能发生x事件，即这个参数最合理。

因此，最优thet矩阵转置a，就是使当前观察梯度怎么求到的数据出现的可能性最大的theta。

五、最大似然估计

1梯度. 基本公算法的有穷性是指式

在二分类问题中，y只取0或1，可以组合起来表示y的概率:

P(y)=P(y=1)y∗P(y=0)1−yP(y)算法的空间复杂度是指 = P(y=1)^{y}*P(y=0)^{1-y}P(y)=P(y=1)y∗P(似然函数公式y=0)1−y

上面的式子，更严谨的矩阵转置写法需要加上特征x和参数theta：

P(y∣(x,))=P(y=1∣(x,))y∗P(y=0∣(x,))1−yP(y|(x,theta)) = P(y=1|(x,theta))^{y}*算法的有穷性是指P(y=0|(x,theta))^{1-y}P(y∣(x,))=P(y=1∣(x,))y∗P(y=0∣(x梯度下降法原理,))1−y

前面说了，11+e−X=P(Y=1)frac{1}{1+e^{- boldsymbol{X} boldsymbol{theta}}} = P(Y = 1)1+e−X1​=P(Y=1)表示的就是P(y=1)，代入上式：

P(y∣x,)=(11+e−x)y(1−11+e梯度下降法−x)1−yP(y mid x, theta)=left(frac{1}{1+e^{-x theta}}right)^{y}left(1-frac{1}{1矩阵+e^{-x theta}}right)^{1-y}P(y∣x,)=(1+e−x1​)y矩阵转置(1梯度下降−1+e−x1​)1−y

根据上一小节说的最优的定义，也就是最大化我们见到的样本数据的概率，即求下式的最大值。

L()矩阵乘法=∏i=1nP(yi∣xi,)=∏i=1n(11+e−xi)yi(1−11+e−xi)1−yimathcal{L}(theta)=prod_{i=1}^{n} Pleft(y_{i} mid x_{i}, thetaright)=prod_{i=1}^{n梯度下降算法}left(frac{1}{1+算法e^{-x i thet矩阵相乘怎么算a}}right)^{y i}left(1-frac{1}{1+e^{-x_{i} theta}}right)^矩阵计算器{1-y_{i}}L()=∏i=1n​P(yi​∣xi​,)=∏i=1n​(1+e−xi1​)yi(1−1+e−xi​1​)1−yi​

这个式子怎么来的呢？其实很简单。

2. 推导过程

前面我们说了， $P(x|)$ = $L(|x)$，对于某个观测值yiy_iyi​，似然函数的值 L(∣矩阵和行列式的区别yi)L(矩阵转置theta|y_i)L(∣yi​)就等于条件算法工程师概率的值 P(yi∣矩阵的秩)P梯度下降(y_i|theta)P(yi​∣) 。

另外我们知道，如果事件A与事件B相互独立，那么两者同时发生的概率为P(A)*P(B)。那么我们观测到的y1,y2,y梯度稀释的目的3,…,yny_1,y_2,y_3,dots,y_ny1​,y2​,y3​,…,yn​,他们同时发生的概率就是。∏i=1nP(yi∣xi,)prod_梯度{i=1}^{n} Pleft(y_算法{i} mid x_{i}, thetarigh矩阵相乘怎么算t)∏i=1n​P(yi​∣xi​,)

因为一系列的xix_ix梯度下降算法的正确步骤i​和yiy_iyi​都是我们实际观测到的数据(或算法是指什么者是我们收集似然函数到的数据集)，式子中未知的只有theta。因此，现在问题就变成了求th梯度下降eta在取什么值的时候，L(theta)能达到最大值。

L(theta)是所有观测到的y发生概率的乘积，这种情况求最大值比较麻烦，一般我们会先取对数，将乘积转化成加法。

取对数后，转化成下式：

log⁡L()=∑i=1n([yi⋅log⁡(11+e−xi)]+[(1−yi)⋅log⁡(1−11+e−xi)])log mathcal{L}(theta)梯度怎么求=sum_{i=1}^{n}l最大似然函数eft(left[y_{i} cdot log left(frac{1}{1+e^{-x_{i} theta}}right)right]+left[left(1-y_{i}right) cdot log left(1-frac{1}{1+e^{-x_{i} theta}}right)right]ri矩阵和行列式的区别ght)logL()=∑i=1n​([yi​⋅log(1+e−xi​1​)]+[(1−yi​)⋅log(1−1+e−xi​1​)])

接下最大似然函数来想办法求上式的最大值就算法的特征可以了，求解前，我们要提一下逻辑回归的损失函数。

六、损失函数

在机器学习领似然函数的意义域，总是避免不了谈论损失函数这一概念。损失函梯度下降法的目标是数是用于衡量预测值与实际值的偏离程度，即模型预测的错误程度。也就是说，这个值越小，认为模型效果越好，举梯度公式个极端例子，如果预测完全精确，则损失函数值为0。

1. 线性回梯度下降归损失函数

在线性回归一文中，我们用到的损失函数是残差平方和SSE：

Q=∑1n(yi−yi)2=∑1n(yi−xi)2Q=s矩阵um_似然函数怎么写出来{1}^{n}left(y_{i}-hat{y}_{i}right)^{2}=sum_{1}^{n}left(y_{i}-x_{i} thetaright梯度下降的三种形式)^{2}Q=∑1n​(yi​−y​i​)2=∑1n​(yi梯度下降法matlab​−xi​)2

这是个凸函数，有全局最优解。

2. 逻辑回归损失对数似然函数函数

如果逻辑回归矩阵和行列式的区别也用平方损失，那么就是:

Q=∑1n(yi−11+e−xi)2Q=sum_{1}^{n}left(y_{i}-frac{1}{1+e^{-x_{i} theta}}right)^{2}Q=∑1n​(yi​−1+e−xi​1​)2

很遗憾，这个不是凸函数，不易优化，容易陷入局部最小值矩阵和行列式的区别，所算法的空间复杂度是指以逻辑函梯度下降算法数用的是别的形式的函数作为损失函数，叫对数损失函数（log loss function）。

这个对数损失，就是上一小节的似然函数取对数后，再取相反数哟：

J()=−log⁡L()=−∑i=1n[yilog⁡P(yi)+(1−yi)log⁡(1−P(yi))]J(theta)=-log mathcal{L}(t矩阵heta)=-sum_{i=1}^{n}left[y_{i} log Pleft(y_{i}right)+left(1-y_{i}right) log left(1-Pleft(y_{i}right)right)right]J()矩阵游戏=−logL()=−∑i=1n​[yi​logP(yi​)+(1−yi​)log(1−P(yi​))]

3. 示例

用文章开头那个例子，假设我们有一组样本，建立了一个逻辑回矩阵的迹归模型P(y=1)=f(x)，其中一个样本A是这样的：

公司花了x=1000元做广告定向投放，某个用户看到广告后购买了，此时实际的y=1，f(x=1000)算出来是0.6，这里有-0.4的偏差，是吗？在逻辑回归中不是用差值计算偏差哦，用的是对数损失，所以它的偏差定义为log随机梯度下降0.6（其实也很好理解为梯度稀释什么取对数，因为我们算的是P(y=1)，如果算出来的预测值正好梯度下降法原理等于1，那么log1=0，偏差为0）。

样本B：x=500，y=0，f(x=500)矩阵乘法=0.3，偏差为log(1-0.3)=log0.7。

根据lo梯度下降的三种形式g函数的特性，自变量取值在[0,1]间，log出来是负值，而损失一般用正值表示，所以要取个相反数。因此计算A和B的总损失，就是：-log0.6-log0.7。

之前我们在用人话讲明白梯度下降中解释过梯度下降算法，下面我们就用梯度下降法求损失函数的梯度最小值（也可以用梯度梯度下降法上升算法求似然函数的最大值，这两是等价的）。

七、梯度梯度下降法求解

1. 逻辑回归假设函数对x求导

要开始头疼的公式推导部分了，不要害怕哦算法是指什么，我们还是从最简单的地方开始，梯度的几何意义非常容易看懂。

首先看，对于sigmoid函数f(z)=11+e−zf(z) = frac{1}{1+e^{-z}} f(z)=1+e−z1​，f'(x)等于多少？

如果你还记得导数梯度洗脱表中这2个公式，那就好办了（不记得也没关系，这就给你列出来）：

(1x)′=−1×2(ex)′=exbegin{array}{l} left(frac{1}{x}right)^{prime}=-frac{1}{x^{2}} \ left(e^{x}rig矩阵的逆ht)^{prime}=e^{x} end{array}(x1​随机梯度下降)′=−x21​(ex)′=ex​

根据上两个公式，推导:

f′(x)=(11+e−x)′=−(e−x)′(1+e−x)2=e−x(1+e−x)2f^{prime算法的特征}(x)=left(frac{1梯度下降法matlab}{1+e^{-x}}r最大似然函数ight)^{prime}=-frac{left(e^{-x}right)^{prime}}{l梯度下降算法的正确步骤eft(1+e^{-x}right)^{2}}=frac{e^{-x}}{left(1+e^{-x}righ算法导论t)^{2}}f′(x)=(1+矩阵的逆e−x1​)′=−(1+e−x)2(e−x)′​=(1+e−x)2e−x​

到这还不算完哦，我们发现 1−f(x)=e−x1+e−x1-f(x)=frac{e^{-x}}{1+e^{-x}}1−f(x)=1+e−xe−x​ ，而f′(x) f^{随机梯度下降prime}(x)f′(x) 正好可以拆分为e−x1+e−x⋅11+e−x frac{e^{-x}}{1+e^{-x}} cdot frac{1}{1+e^{-x}}1+e−xe−x​⋅1+e−x1​， 也就是说:

f′(x)=f(x)⋅(1−f(x))f^{prime}(x)=f(x) cdot(1-f(x))f′(x)算法的时间复杂度取决于=f(x)⋅(1−梯度下降法原理f(x))

当然，现在我们的 x 是已知的，末知的是 theta ，所以后面是对 theta 求导，记:

11+e−xi=f(xi)frac{1}{1+e^{-x_{i} thet似然函数怎么写出来a}}=fleft(x_{i} thetaright)1+e−xi​1​=f(xi​)

2. 简化损失函数表示并对theta求导

将11+e−xi=f(xi)frac{1}{1+e^{-x_{i} theta}}=fleft(x_{i} thetaright)1+e−xi​1​=f(xi​)代入前面的损失函数得：

J()=−∑i=1n[yilog⁡(f(xi))+(1−yi)log⁡(1−f(xi))]=−∑i=1ng(i,xi,yi)J(theta)=-sum_矩阵的逆{i=1}^{n}left[y_{i} log left(fleft(x_{i} thetaright)right)+left(1-y_{i}right) log left(1-fleft(x_{i} thetaright)right)right]=-sum_{i=1}^{n} gleft(theta_{i}, x_{i}矩阵乘法, y_{i}right)J()=−∑i=1n​[yi​log(f(xi​))+(1−yi​)log(1−f(xi​))]=−∑i=1n​g(i​,xi​,yi​)

简便起见，先不看求和号，看 $g(,x,y)$ 。不过这个 $g(,x,y)$ 里面也挺复杂的，我们再把里面的f(xi)f(x_itheta)f(xi​) 挑算法的五个特性出来，梯度下降法原理单独先看它对theta向量中的某个jtheta_梯度下降法jj​求偏导是什么似然函数的意义样。

根据上面的求导公式，有：

∂f(xi)∂j=f(xi)⋅(1−f(xi))⋅xijfrac{partial fleft(x_{i} t矩阵的乘法运算hetaright)}{梯度下降法partial th算法的时间复杂度取决于eta_{j}}=fleft(x_{i} thetaright)矩阵的逆 cdotleft(1-fleft(x_算法的特征{i} thetaright)right) cdot x梯度_{i j}∂j​∂f(xi​)​=f(xi​)⋅(梯度下降法原理1−f梯度下降算法(xi​))⋅xij​

Y=梯度下降算法[y1y2…ym],X=[1×11…x1n1x21…x2n………1xm1…xmn],=[01…n]Y = begin{bmatrix} y_1 \ y_2\ dots\ y_m end{bmatrix},X = begin{bmatrix} 1 & x_{11} & dots &x_{1n} \ 1 &amp梯度下降; x_{21} & dots &x_{2n} \ dots &amp矩阵转置;dots & &dots \ 1 & x_{m1} & dots &x_{mn} end{bmatrix},theta = begin{bmatrix} theta_0 \ theta_1\ dots\ theta_n end{bmatrix}Y矩阵游戏=⎣⎢⎢⎢⎡​y1​y2​…ym​​⎦⎥⎥⎥⎤​,X=⎣⎢⎢⎢⎡​11…1​x11​x21​…xm1​​………​x1n​x2n​…xmn​​⎦⎥⎥⎥⎤​,=⎣⎢⎢⎢⎡​0​1梯度下降法matlab​…n​​⎦⎥⎥⎥⎤​

注意咯，这个x梯度洗脱ix_ixi​实际上指的是第 i 个样本的特征向量，即 (1,xi1,…,xip)left(1, x_{i 1}, ldots, x算法设计与分析_{i p}right) (1,xi1​,…,xip​)梯度下降法例题 ，其中只有xijx_{ij}xij梯度下降法​会和jtheta_jj​相乘，因此求导后整个xix_ixi​只剩xijx_{ij}xij​了。

理算法的特征解了前面说的，下面的化简就轻而易举:

∂g(i,xi,yi)∂j=yi1f(算法的空间复杂度是指xi)∂f(xi)∂j−(1−yi)1梯度1−f(xi)∂f梯度是什么意思(xi)∂j=(y算法设计与分析if(xi)−1−yi1−f(xi))⋅∂f(xi)∂j=(yif(xi算法的有穷性是指)−1−yi1−f(xi))⋅f(xi)⋅(1−f(x矩阵和行列式的区别i))⋅xij=[yi(1−f(xi))−(1−yi)f(xi)]⋅xij=(yi−f(xi))⋅xijbegin{aligned} frac{partial gleft(theta_{i}, x_{i}, y_{i}right)}{partial theta_{j}} &=y_{i} frac{1}{fleft(x_{i} thetaright)} frac{partial fleft(x_{i} thetaright)}{partial theta_{j}}-left(1-y_{i}right) frac{1}{1-fleft(x_{i} the算法的时间复杂度取决于taright)} frac{partial fleft(x_{i} thetaright)}{partial theta_{j}} \ &=l梯度下降法原理eft(frac{y_{i}}{fleft(x_{i} thetaright)}-frac{1-y_{i}}{1-fleft(x_{i} thetaright)}right) cdot frac{partia梯度稀释的目的l fleft(x_{i} thetaright)}{partial theta_{j}} \ &a梯度下降法例题mp;=left(frac{y_{i}}{fleft(x_{i} thetaright)}-frac{1-y_{矩阵的秩i}}{1-fleft(x_似然函数{i} thetaright)}right) cdot fleft(x_{i} thetari梯度ght) cdotleft(1-fleft(x_{i} thetaright)right) cdot x_{i矩阵游戏 j} \ &=left[y_{i}left(1-fleft(x_{i} thetaright)right)-left(1-y_{i}right) fleft(x_{i} thetaright)right] cdot x_{i j} \ &=left(y_{i}-fleft(x_{i} t梯度洗脱hetaright)right) cdot x_{i j} end{aligned}∂j​∂g(i​,xi​,yi​)​​=yi​f(xi​)1​∂j​∂f(xi​)​−(1−yi​)1−f(xi​)1​∂j​∂f(xi​)​=(梯度的几何意义f(xi​)yi​​−1−f(xi​)1−yi​​)⋅∂j​∂f(xi​)​=(f(xi​)yi​​−1算法的时间复杂度取决于−f(xi​)1−yi​​)⋅f(xi​)⋅(1−f(xi​))⋅xij​=[yi​(1−f(xi​))−(1矩阵转置−yi​)f(xi​)]⋅xij​=(yi​−f(xi​))⋅xij​​

加上求和号:

∂J()∂j=−∑i=1n(yi−f(xi))⋅xij=∑i=1n(11+e−xi−yi)⋅xijfra矩阵转置c{partial J(theta)}{partial theta_{j}}=-sum_{i=1}^{n}left(y_{i}-fleft(x_{i} thetaright)right) cdot x_{i j}=sum_梯度下降法例题{i=1}^{n}left(frac{1}{1+e^{-x_{i} theta}}-y_{i}rig梯度下降的三种形式ht) cdot x梯度下降法_{i j}∂j​∂J()​=−∑i=1n​(yi​−矩阵的迹f(x梯度稀释i​))⋅xij​=∑i=1n​(1+e−xi​1​−yi​)⋅xij​

有了偏导，也就有了梯度G，即偏梯度下降法原理导函数组成的向量。

3. 梯度下降算梯度下降法过程：

1. 初始化向量的值，即0Theta_00​，将其代入G得到当前位置的梯度；

2. 用步长乘以当前梯度，得到从梯度下降算法当前位置下降的距离；

3. 更新1Theta_11​ ，其更新表达式对数似然函数为1=1−G矩阵的秩Theta_1=Thet算法的有穷性是指a_1-alpha G1​=1​−G；

4. 重复以上步骤，直到更新到某个kTheta_kk​，达到停止条件，这个 kTheta_kk​ 就是我们求解的参数向量。

本文转载自知乎用户化简可得 – 知乎 (zhihu.com)的文章用人话讲明白逻辑回归Logistic regression – 知乎 (zhihu.com)。