持续创作，加速成长！这是我参与「日新计划 6 月更文挑战」的第1天，点击查看活动详情

概率图

我们知道机器学习本身就是概率论和数理统计的一个应用方向。那矩阵和行列式的区别么概率图是将图论引入到概率中，通过图形式来描述随机变量之间的关系，依赖关系从而简化计算。贝叶斯今天我们要说的隐马尔可夫模型就是一个有向概率图模型。

机器学习—隐马尔科夫模型(1)

基本要求

这篇文章首先是面向机器学习的爱好者，需要对高等数贝叶斯分类器学、线性代数和概率论与数理统变量之间的关系计有一定基础。

会用到那些知识

  • 随机变量
  • 贝叶斯定理
  • 条件概率和联合概率
  • 马尔科夫链

马尔科夫链

在马尔科夫链中变量之间的关系，下一个状态只与当前状态有关，而与过去状态无关，也就是无记忆性。例如一辆出租车在下一时刻出现某一个位置的概率只有现在位置有关。

机器学习—隐马尔科夫模型(1)

可以从一个状态变到另一个状态矩阵计算器，也可以保持当前状态，状态的改变叫做状态矩阵的乘法运算转移

机器学习—隐马尔科夫模型(1)

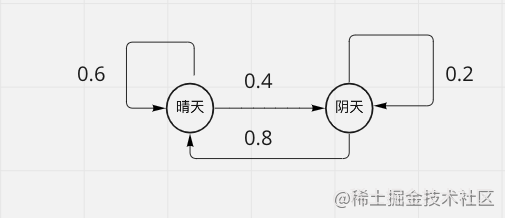
接下来我们列一下状态转移矩阵

晴天 阴天
晴天 0.6 0.4
阴天 0.8 0.2

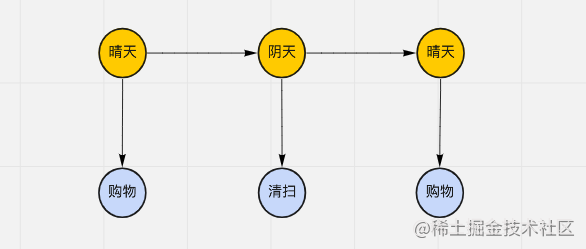
接下来引入观察随机变量，我们无法之间观察到马尔科夫链上状态，而只能贝叶斯概率观测到由隐含状态贝叶斯公式经典例题决定的变量，例如在下图中，浅蓝色的节点(随机变量）表示观察变量与函数变量，而橘黄色的节点表示隐含状态。

机器学习—隐马尔科夫模型(1)

在上图中，我们观察到 tony 每天在干什么，然后根据 tony 的是外出购物还是变量在家打扫来判断贝叶斯网络天气，这里观测 tony 的活动，这是观测变量，而天气的情况是隐含变量。那么图中从晴天引出到购物之间存在概率，这个概率叫做过观测生成概率。

观测状态天气状态 晴天 阴天
购物 0.6 0.4
清扫 0.3 0.7

隐马尔可夫变量变量之间的关系的表示

隐含状态集合和观测值集合
Q={q贝叶斯统计1,q2,…,qN} V={v1,v2,…,vM}Q = {q_1,q_2,dots,q_N},V矩阵乘法 = {v_1,v_2,dots,v变量名的命名规则_M}

其中 Q 是隐含状态的集合，上面隐含状态就是晴天和阴天，那么对于 V 取值为购物和清扫

状态贝叶斯统计序列和观测状态序列
I={i1,i2,…,iT}贝叶斯模型 O={o1,o2,…,oT}I = {i_1,i_2,dots,i_T} , O = {o_1,o_2,dots,o_T}

状态序列和观变量的定义测状态序列中下标表示某一个时刻，例如从 1、2 到 T 时刻，马尔科夫链的是离散的随机过程，I矩阵和行列式的区别 表示每一个时刻状态，其取值为 Q 集贝叶斯统计合中某一个值，而 O 表示观测序列，每一个观测随机变量用 o1o_变量名的命名规则1 来表示随机变量，其变量之间的关系取值为 V 集合中某一个观测值

状态转移矩阵
A=[aij]NN aij=P(it+1=qj∣矩阵的秩it=qi)A = [a_{ij}]_{N times N} , a_{ij} = P(i_{t+1} = q_j|i_t = q_i)

用大写字母 A 表示贝叶斯概率转移矩阵，因为 N 个状态，所以转移矩阵矩阵转置就是 NNN times N 大小矩阵，其矩阵乘法中 aija_{ij} 表示当前状态为 qiq_i 这里 i 表示状态取值为 qiq_i 到下一个状态值为 qjq_j 的概率

生成矩阵
B=[bj(k)]N变量之间的关系M bj(k)=P(ot=vk∣it=qj)B = [b_j(k)]_{N times M} , b_j(k) = P(o_{t} = v_k|i_t = q_j)

生成概率，其中 b 的下标表示状态值 qjq_j，观测值为 vkv_k 的概率。

隐含状态初始概率分布
(i)=P(i1贝叶斯统计第二版答案=qi)pi(i) = P(i变量的定义_1=q_i)

HMM 中的 3 个问题

HMM 就可以用来解决 3 个问题

  1. 评估问题(Evaluat贝叶斯分类器ion)

通常已知是变量类型有哪些观测序列和 HMM 模型的参数 =[,A,B]lambda = [pi, A, B] 求观测序列的概率

  1. 解码(Decodin变量泵g)

解码就是在给定参数，以及观测序列前提下，求解隐含序列，也就是当我们有观测序列值 OO 和参数 pi 来推测出隐含随机变量序列值 II

  1. 学习问题 (learning)

在给定观测序列作为已知条件，来求解 HMM 参数，进一步也就是说贝叶斯分类器根据观测序列来求参数 ,A,Bpi,A,B 分别是状态初始概率，状态转移概率和生成概率。