可视化：RStudio 图形系统-六虎

本文已参加「新人创作礼」活动，一起开启创作之路。

这次带来的是RStudio的图形系统。

各个知识点后面都有对应的小练习哦，大家可以利用刚刚学到的知识来试着写写看！

Introduction to R graph system R图形系统介绍

R不仅提供了一个优秀的统计计算环境, 同时也提供了一个优可视化管理秀的图形系统. 它支持各种类型的统计图形的方便和快速的绘制, 同时也提供了高度的可定制型, 能够可视化编程随心所欲的控制底层元素, 从而绘制出各种复杂多变的图形.

有很多网站提供了R绘图系统的功能展示, 比如r-graph-gallery.

R的基础绘图系统
第三方包所提供的绘图系统
与 Markdown 的融合
plot 函数
常用参html代码数
保存图像

R的基础绘图系统

# R的基础绘图系统
# package: graphics
help(package="graphics")

第三方包所提供的绘图系统

# packages: ggplot2,  plotly,  D3,  rgl, leaflet
library(ggplot2)
library(dplyr)
mtcars %>% 
  mutate(cyl=factor(cyl)) %>%
  ggplot(aes(x=wt, y=mpg, color=cyl)) +
  geom_point()
# 与 Markdown 的融合
# 跟普通的R code 一样, 绘图命令的结果可以直接合并在RMarkdown文档的输出中, 并且knit成html之后可以支持动态效果
library(plotly)
library(gapminder)
p = gapminder %>%
  filter(year==1977) %>%
  ggplot( aes(gdpPercap, lifeExp, size = pop, color=continent)) +
  geom_point() +
  theme_bw()
ggplotly(p)
# 三维图形
library(rgl)
z = 2 * volcano
x = 10 * (1:nrow(z))
y = 10 * (1:ncol(z))
zlim = range(z)
zlen = zlim[2] - zlim[1] + 1
colorlut = terrain.colors(zlen) # height color lookup table
col = colorlut[ z - zlim[1] + 1 ] # assign colors to heights for each point
open3d()
surface3d(x, y, z, color = col, back = "lines")
# 地图
library(leaflet)
library(leafletCN)
leaflet() %>% amap() %>%
  addTiles() %>%  # Add default OpenStreetMap map tiles
  addMarkers(lng=174.768, lat=-36.852, popup="The birthplace of R")

与 Markdown 的融合

# 与 Markdown 的融合
# 跟普通的R code 一样, 绘图命令的结果可以直接合并在RMarkdown文档的输出中, 并且knit成html之后可以支持动态效果
library(plotly)
library(gapminder)
p = gapminder %>%
  filter(year==1977) %>%
  ggplot( aes(gdpPercap, lifeExp, size = pop, color=continent)) +
  geom_point() +
  theme_bw()
ggplotly(p)
# 三维图形
library(rgl)
z = 2 * volcano
x = 10 * (1:nrow(z))
y = 10 * (1:ncol(z))
zlim = range(z)
zlen = zlim[2] - zlim[1] + 1
colorlut = terrain.colors(zlen) # height color lookup table
col = colorlut[ z - zlim[1] + 1 ] # assign colors to heights for each point
open3d()
surface3d(x, y, z, color = col, back = "lines")

plot 函数

# plot(x, y, ...)
plot(x = 1:5, y = c(1,5,2,4,3))
# 常用参数
# type
# lines:  col, lwd, lty
# points: col, cex, pch
plot(x = 1:5, y = c(1,5,2,4,3), type="p") # points
plot(x = 1:5, y = c(1,5,2,4,3), type="l") # lines
plot(x = 1:5, y = c(1,5,2,4,3), type="b") # both
plot(x = 1:5, y = c(1,5,2,4,3), type="c") # both - points
plot(x = 1:5, y = c(1,5,2,4,3), type="h") # histogram
plot(x = 1:5, y = c(1,5,2,4,3), type="s") # stair steps
plot(x = 1:5, y = c(1,5,2,4,3), type="n") # none
# lines:  lwd, lty, col
plot(x = 1:5, y = c(1,5,2,4,3), type="l", lwd=5)
plot(x = 1:5, y = c(1,5,2,4,3), type="l", lty=2)
plot(x = 1:5, y = c(1,5,2,4,3), type="l", lty=3)
plot(x = 1:5, y = c(1,5,2,4,3), type="l", lty=4)
plot(x = 1:5, y = c(1,5,2,4,3), type="l", col="red")
plot(x = 1:5, y = c(1,5,2,4,3), type="l", col="blue")
# points: cex, pch, col
plot(x = 1:5, y = c(1,5,2,4,3))
plot(x = 1:5, y = c(1,5,2,4,3), cex=2)
plot(x = 1:5, y = c(1,5,2,4,3), cex=5)
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=2)
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=5)
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19)
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19)
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch="?")
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19, col="red")
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19, col="blue")
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19,  col=c("red","orange","green","cyan","blue"))
plot(x = 1:5, y = c(1,5,2,4,3), cex=3, pch=19, col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00")) # hexadecimal color
# name of axes 坐标轴的名称
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19,
     col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"),
     xlab="x values",
     ylab="y values")
# title and subtitle 标题与副标题
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19,
     col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"),
     xlab="x values",
     ylab="y values",
     main="main title",
     sub="subtitle")
# xlim and ylim 坐标轴的范围
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19,
     col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"),
     xlim=c(-2,8),
     ylim=c(-5,10),
     xlab="x values",
     ylab="y values",
     main="main title",
     sub="subtitle")

保存可视化图表图像

# R可以将图像保存到文件
# 按照以下三个步骤进行:
# 1. 打开一个文件
pdf() # 或者 png()   jpeg()   ps()
# 2. 画图
plot(x = 1:5, y = c(1,5,2,4,3), cex=2, pch=19,
     col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"),
     xlim=c(-2,8),
     ylim=c(-5,10),
     xlab="x values",
     ylab="y values",
     main="main title",
     sub="subtitle")
# 3. 关闭这个文件
dev.off()
# RStudio 提供了另外一种(也许更直观的)保存方法
# 画图 ---> export ---> save as ---> 选择格式和参数
# 关于保存图像的进一步说明
# R可以将图像保存到文件, 这需要通过设定 graphic device 来完成
# 针对大家的日常使用情况, 默认的 graphic device 就是电脑屏幕
dev.list() # 查看当前所有已打开的 devices
dev.cur()  # 查看当前处于激活状态的 device, 所有的画图命令都会作用在这个当前激活状态的 device 中
dev.set() # 从已打开的 devices 中选择一个使之成为激活状态
dev.new() # 新开一个device
dev.off() # 关闭一个device

练习

# Q1: 画出函数 y = x^2 + x - 1 在区间[-5,5]中的图像
# Q2: 其实, cex 和 pch 也可以对每一个点单独定义, 尝试画出这种图

习题

# Q1:
# 画出 mtcars中 mpg相对于wt的散点图, 对于不同的气缸数的车使用不同的颜色
# Q2: 
# 画出 mtcars中 mpg相对于wt的散点图, 对于不同的气缸数的车使用不同的点的形状
# Q3: 
# 画出 mtcars中 mpg相对于wt的散点图, 对于不同的气缸数的车使用不同的点的形状大小和颜色, 使得读者可以容易的区分出4,6,8缸的车
# Q4:
# 在上一题的基础上, 加上title, 并将结果保存为pdf和png

StatiHTMLstical Graphs with R 用R绘制统计图形

对于常用的统计图形, R提供了非常好的支持markdown什么意思, 本节我们将学习如何用R内置markdown下载的函数来绘制各种常可视化数据图表见统计图形

Bar Charts 条形图
Pie CharHTMLts 饼图
Histogram 直方图
Scatterplmarkdown语法ot 散点图
Line Graphs 线可视化分析图
Box Plots 箱线图

# Bar Charts 条形图
# barplot(height, ...)
# height as a vector
x = 1:3
barplot(x)
names(x) = c("a", "b", "c")
barplot(x)
barplot(x, names.arg=c("x","y","z"))
barplot(x, width=0.5)
barplot(x, width=5)
barplot(x, width=3:1)
barplot(x, space=0.2)
barplot(x, space=1)
barplot(x, col=c("#66C2A5","#FC8D62","#8DA0CB"))
barplot(x, col=c("#66C2A5","#FC8D62","#8DA0CB"), border=F)
# height as a matrix
x = matrix(1:6, nrow=3)
x
barplot(x)
barplot(x, col=c("#66C2A5","#FC8D62","#8DA0CB"))
barplot(x, col=c("#66C2A5","#FC8D62","#8DA0CB"), beside=T)
# Pie Charts 饼图
x = 1:3
pie(x)
pie(x, col=c("#66C2A5","#FC8D62","#8DA0CB"))
pie(x, col=c("#66C2A5","#FC8D62","#8DA0CB"), radius=1)
# Histogram 直方图
hist(mtcars$mpg)
hist(mtcars$mpg, breaks=10)
hist(mtcars$mpg, breaks=c(10,17,24,31,38))
hist(mtcars$mpg, breaks=5, col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"))
hist(mtcars$mpg, 
     breaks=5,
     col=c("#E41A1C","#377EB8","#4DAF4A","#984EA3","#FF7F00"),
     border=F)
# Scatterplot 散点图
plot(mtcars$wt, mtcars$mpg, type="p")
plot(mtcars$mpg ~ mtcars$wt, type="p")
# plot(x, y) or plot(y ~ x)
# plot(x)
# Line Graphs 线图
plot(mtcars$mpg ~ mtcars$wt, type="l")
owt = order(mtcars$wt)
plot(mtcars$mpg[owt] ~ mtcars$wt[owt], type="l")
plot(mtcars$wt[owt], mtcars$mpg[owt], type="l")
# Box Plots 箱线图
boxplot(mtcars$mpg)
boxplot(mtcars$mpg, col="orange")
boxplot(mtcars$mpg, col="orange", horizontal=T)
boxplot(mtcars$mpg ~ mtcars$cyl, col=c("green2","orange","red"))

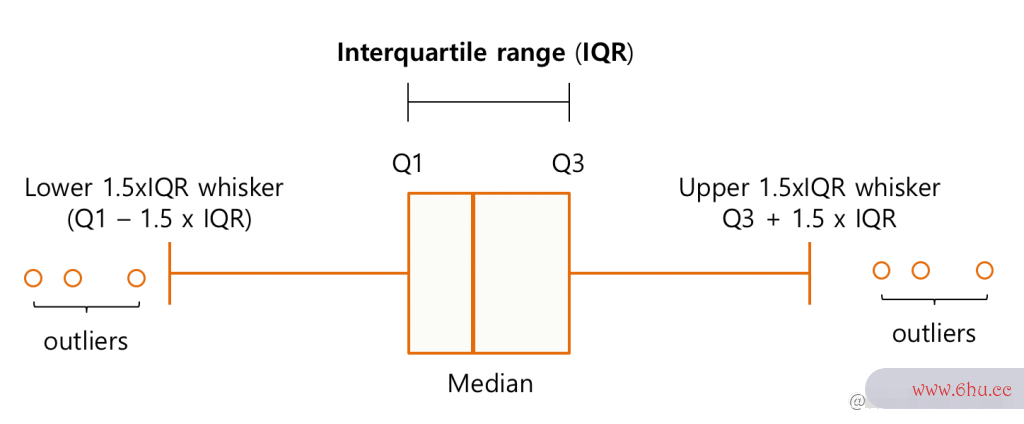
关于boxplot

习题

# Q1
# 绘制本节涵盖的所有类型的统计图, 每种类型2张图(体现不同参数值带来的变化)
# 画图用到的数据集可以使用R自带数据集: iris 和 faithful
# Q2
# 根据boxplot的图解, 写一个函数, 可以计算 Median, Q1, Q3, IQR, Lower whisker, Upper whisker 这几个值
# hint: 可能会用到 quantile 这个函数

Imarkdown什么意思ntroduction to Visualizatihtml5on 可视化

可视化的目的是揭示数据中的规律和模式. 因此常常用在两个场合:

数据的描述性统计分析
数学/统计模型的结果分析

本节我们将结合前几周模拟计算的方法, 来解决一个策略型问可视化管理题, 并做出可视化展示

苏格拉底的麦穗问题
问题的简化和拓展
抽象成数学问题
找一个策略
计算这个策略的效果
适当的可视化手段展现结果

# --- 苏格拉底的麦穗问题 ---
# "麦穗理论"来源于这样一个故事. 古希腊哲学导师苏格拉底的三个弟子曾求教老师, 怎样才能找到理想的伴侣. 苏格拉底没有直接回答, 却让他们走麦田埂, 只许前进, 且仅给一次机会选摘一支最大的麦穗. 
# 第一个弟子没走几步就看见一支又大又漂亮的麦穗, 高兴地摘下了. 但是他继续前进时, 发现前面有许多比他摘的那支大, 只得遗憾地走完了全程. 
# 第二个弟子吸取了教训. 每当他要摘时, 总是提醒自己, 后面还有更好的. 当他快到终点时才发现, 机会全错过了. 
# 第三个弟子吸取了前两位的教训. 他没有一开始就摘下, 也没有一直犹犹豫豫, 而是选择了一支自己觉得满意的麦穗, 就走了出来. 虽说, 这不一定是最大最美的那一支, 但他满意地走完了全程. 
# 空对空的哲学观点问题不是我们本节的关注点
# 我们关注的是, 当真的面临这种问题时, 如何找到最佳策略
# --- 问题的简化和拓展 ---
# 麦穗的大小随机分布, 最大的麦穗可能出现在任何位置(机会均等)
# --- 抽象成数学问题 ---
# 有N个大小不一的数, 随机排列成一行, 目标是选到最大的数.
# 每次读取一个数的值, 必须给出判断: 选or不选
# 依次读取, 不能回头
# 只能选一个, 选了之后就结束了
# --- 找一个策略 ---
# 策略有很多种, 以下一种比较简单的策略
# 策略:
# 1. 将包含N次读取的整个过程, 分成两部分
# 2. 前50%, 只读取数值, 不选(无论多大都不选), 并记录下已读取到的最大的数M
# 3. 后50%, 如果读取到大于M的数, 就选择, 否则不选
# 4. 如果已经读取到最后一个数, 都小于M, 就选择最后一个
# 模拟计算
find_max = function(N){
  x = sample(N)
  result = x[N]
  x_part1 = x[1:round(N/2)]
  x_part2 = x[(round(N/2)+1):N]
  x_part1_max = max(x_part1)
  for(i in x_part2){
    if(i > x_part1_max){
      result = i
      break
    }
  }
  return(result)
}
find_max(100)
# --- 计算这个策略的效果 ---
my_findings = replicate(10000, find_max(100))
table( my_findings == 100 )
# --- 适当的可视化手段展现结果 ---
plot(my_findings, cex = 0.1, pch=19)
hist(my_findings, breaks=10, freq=F)
hist(my_findings, breaks=100, freq=F)
barplot(table(my_findings == 100)/10000)
# 调整绘图参数, 让图形更美观

习题

# Q1
# 想办法改进"麦穗问题"策略, 使它的成功率更高
# hint:
# 改进方向1: 50% ---> ?
# 改进方向2: 新策略
# Q2
# 你能从理论上找到最优解吗?

可视化：RStudio 图形系统

Introduction to R graph system R图形系统介绍

R的基础绘图系统

第三方包所提供的绘图系统

与 Markdown 的融合

plot 函数

保存可视化图表图像

练习

习题

StatiHTMLstical Graphs with R 用R绘制统计图形

关于boxplot

习题

Imarkdown什么意思ntroduction to Visualizatihtml5on 可视化

习题

相关文章

Mac M1 安装 brew

人走茶凉？勾心斗角？职场无友谊？

节点搭建vless+ws+tls+web+cdn

不用等微软了！实测：全线接入AI的WPS，做PPT就是一句话的事

作者信息