本文已参与「新人创作礼」活动,一起开启创作之路
在进入正式话题之前需要引入四个概念:稳态误差、终值定理、幅角条件和系统稳定的充要条件。
稳态误差:系统达到稳定状态后,系统的实际输出量与系统希望的输出量之间的偏差。
终值定理:设有连续函数f(t)f(t)f(t),当t趋于无穷时,f(t)f(t)f(t)的极限存在,则有
 其中,F(s)F(s)F(s)是f(t)f(t)f(t)经过拉普拉斯变换后的函数,即
其中,F(s)F(s)F(s)是f(t)f(t)f(t)经过拉普拉斯变换后的函数,即

幅角条件
零点到根的夹角和与极点到根的夹角和是 180180180 的倍数。表示极点,表示零点
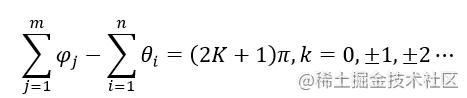
系统稳定的充要条件:闭环传递函数的极点位于sss的左半平面。对于某个系统的传递函数的极点为 ppp1 和 ppp2 ,它们都在实轴上,即 p1 === -$$a , p2 === -$$b (aaa 、bbb均为常数)对该系统一个单位冲激信号,于是系统的响应为
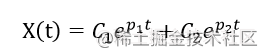 当 ppp
当 ppp1 <<< 000 , ppp2 <<< 000 时
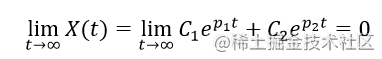 说明这个系统是收敛的,也就是说这个系统可以稳定。
说明这个系统是收敛的,也就是说这个系统可以稳定。
当 ppp1 与 ppp2 有一个大于000 时
 说明这个系统是发散的,也就是说这个系统无法达到稳定。
当 ppp
说明这个系统是发散的,也就是说这个系统无法达到稳定。
当 ppp1 与 ppp2 并没有在实轴上,即 p1 === -$$a +++ b$$i , p2 === -$$a -$$b$$i ,此时有
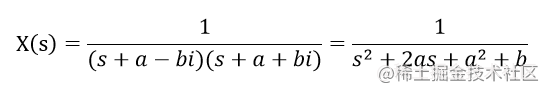 在经过拉普拉斯逆变换,得
在经过拉普拉斯逆变换,得
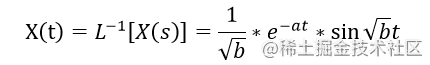 正弦函数是等幅振荡函数,而 eee^(-at)^ 会随 ttt 得增大而减小 ,最终趋向于000,故而 X(t)X(t)X(t) 是一个振荡衰减函数,最终仍会趋向于 000。图像大概是这个样子
正弦函数是等幅振荡函数,而 eee^(-at)^ 会随 ttt 得增大而减小 ,最终趋向于000,故而 X(t)X(t)X(t) 是一个振荡衰减函数,最终仍会趋向于 000。图像大概是这个样子
 如果 p
如果 p1 === aaa +++ bibibi , p2 =a−bi= a -bi=a−bi ,此时有
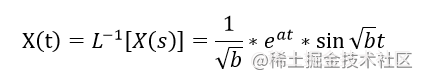 此时该函数时振荡发散的,是不稳定的,图像就是上图从右往左看。
此时该函数时振荡发散的,是不稳定的,图像就是上图从右往左看。
进入正式话题,在做实际工程或者学习自动控制原理的时候,PID控制经常被提起,大部分工程中涉及控制基本都是PID,那么PID到底是什么?它为什么可以做控制使用?又是如何控制的呢?所谓PID就是比例积分微分控制,下面我们就对333种控制稍做分析。
比例控制
对于如下比例控制系统,输入是R(s)R(s)R(s),输出是X(s)X(s)X(s),
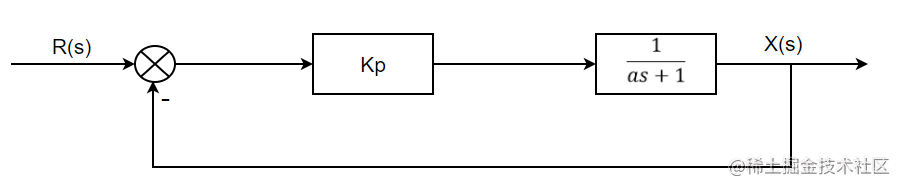 有
有
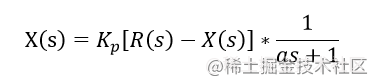 于是系统的闭环传递函数为
于是系统的闭环传递函数为
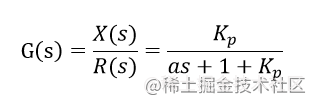 由这个传递函数可知极点p=(−1−p = ( -1 –p=(−1− K
由这个传递函数可知极点p=(−1−p = ( -1 –p=(−1− Kp )/a) /a)/a,我们知道,当 ppp位于 sss 的左半平面时系统才会稳定,也就是说 Kp >>> −1-1−1 时系统才会稳定。
我们给系统一个输入一个目标值,即 r(t)=rr(t)=rr(t)=r, 于是
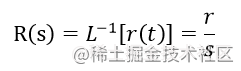 则
则
 根据中值定理,有
根据中值定理,有
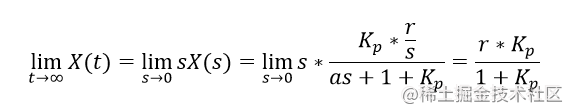 那么稳态误差为
那么稳态误差为
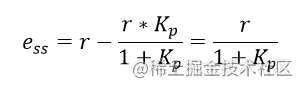 由上式可知,KKK
由上式可知,KKKp 趋向于无穷大时,eeess 趋向于 000,但实际工程中,KKKp 不可能取太大,否则超调量会非常大(一阶系统除外),如果超过了控制器的输出范围,那也就没有意义了,但是在控制器的输出范围内,Kp又不会太大,所以稳态误差还是消除不了,故而一般不单独使用比例控制。
举个实际的例子:
对于系统:
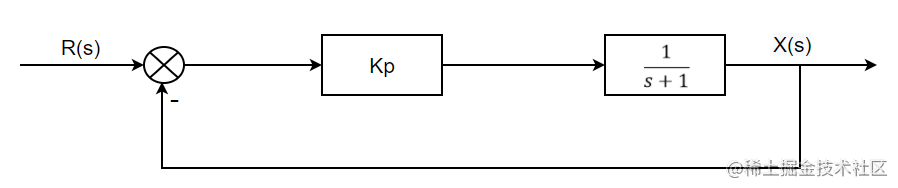 通过以上的推理,该系统在 KKK
通过以上的推理,该系统在 KKKp >>> −1-1−1 时才会稳定,那就在simulink中仿真一下,把输入设置为101010,示波器中的黄线代表目标值,蓝线代表输出值:
KKKp === −-− 222 时,系统结构如下
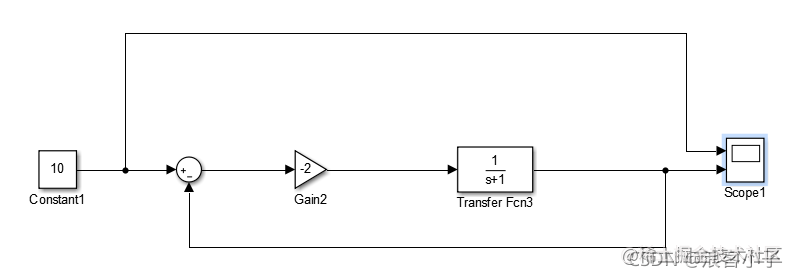 输出曲线如下
输出曲线如下
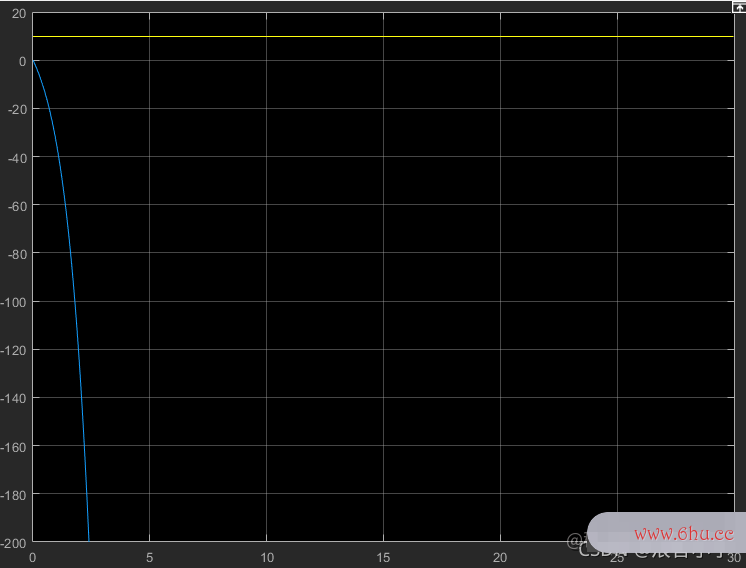 由图可以看出,输出值已经跑飞了,系统不可能会稳定下来。
看看 KKK
由图可以看出,输出值已经跑飞了,系统不可能会稳定下来。
看看 KKKp === 222 时的情况
 这时候系统已经稳定了,但是稳态误差很大。
再看看 KKK
这时候系统已经稳定了,但是稳态误差很大。
再看看 KKKp === 100 的情况
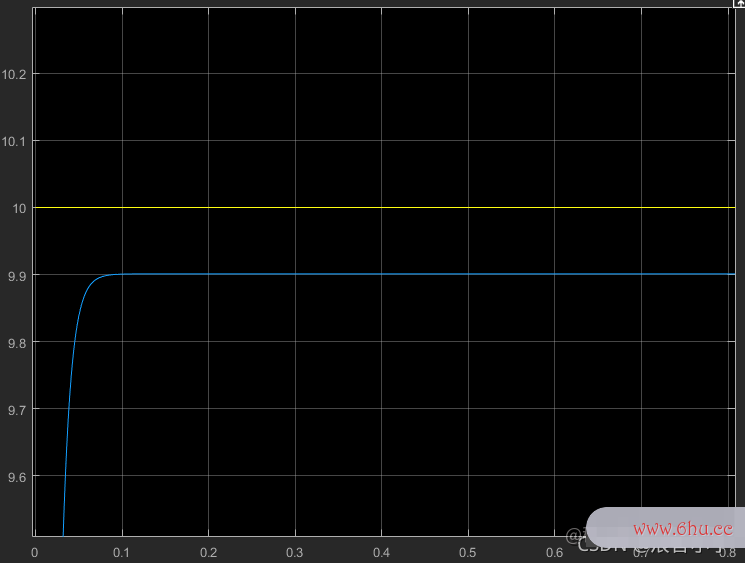 此时稳态误差已经很小了,可以忽略不计了。但是此时的 KKK
此时稳态误差已经很小了,可以忽略不计了。但是此时的 KKKp 已经非常大了,如果系统此时输出为 999 ,那么偏差就为 111,比例控制输出为 100100100,对于PWM调节的话,占空比最大就是100$$%,很明显这是不符合实际应用的。当然控制器的输出我们可以不当做占空比直接使用,比如在单片机的PWM的配置过程中,令计数值为100010001000才代表100$$%占空比,那么比例控制输出100100100,对应PWM占空比也才10$$%,看上去很合理,也符合实际应用,这样一来,系统的调节时间就会变长,同样我们也可以理解为此时 KKKp 还较小。所以比例控制一般不单独使用。
积分控制
上面我们研究了比例控制器,他不能消除稳态误差,所以需要设计新的控制器C(s)C(s)C(s),系统结构框图如下:
 求得系统传递函数
求得系统传递函数
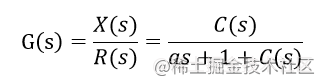 我们同样令r(t)=rr(t) = rr(t)=r ,拉普拉斯变换后, R(s)=r/sR(s) = r / sR(s)=r/s,于是有
我们同样令r(t)=rr(t) = rr(t)=r ,拉普拉斯变换后, R(s)=r/sR(s) = r / sR(s)=r/s,于是有
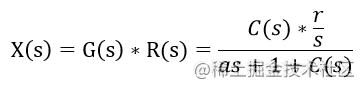 我们的目标是消除稳态误差,即 eee
我们的目标是消除稳态误差,即 eeess === 000
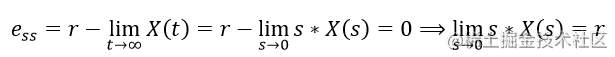 继续推导
继续推导
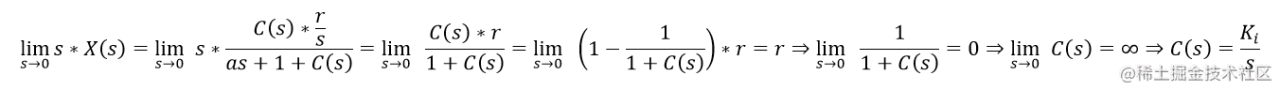 这个 C(s)C(s)C(s)不就是积分嘛,KKK
这个 C(s)C(s)C(s)不就是积分嘛,KKKi 就是积分增益。我们来验证一下,还是拿前面的系统
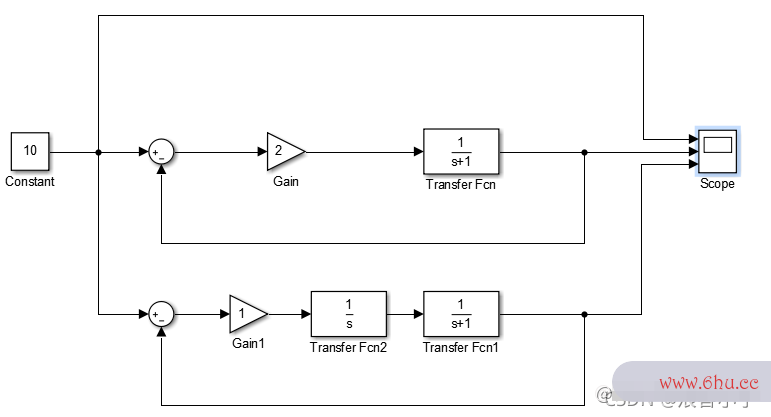 设置 KKK
设置 KKKp === 222 , KKKi === 111,看看比例控制与积分控制的效果
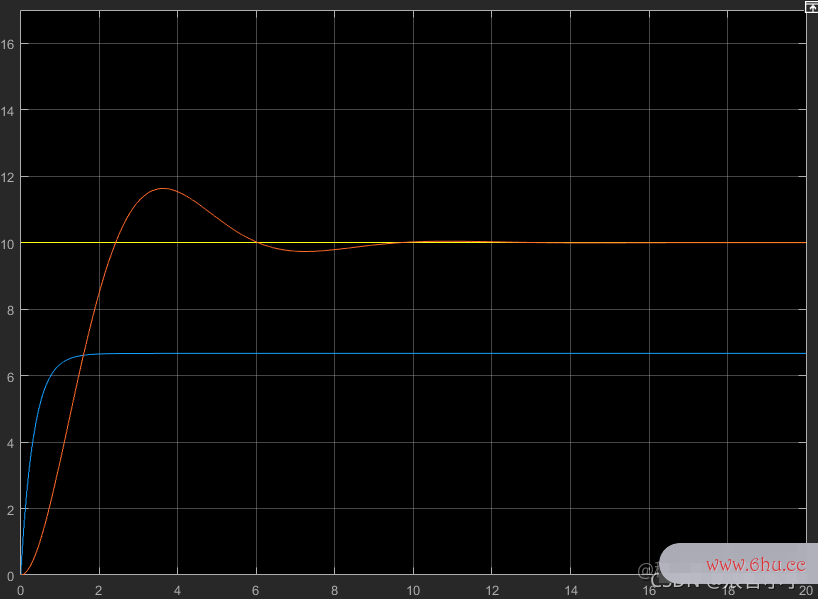 黄色的直线表示目标值,蓝色的线是比例控制,橙色线是积分控制。由图可以看出,积分控制很明显的消除了稳态误差,但是积分控制的调节时间却比比例控制要长很多,那将比例控制与积分控制放在一起,同时作用,效果又是怎样的?
黄色的直线表示目标值,蓝色的线是比例控制,橙色线是积分控制。由图可以看出,积分控制很明显的消除了稳态误差,但是积分控制的调节时间却比比例控制要长很多,那将比例控制与积分控制放在一起,同时作用,效果又是怎样的?
更改系统框图
 最上面一个闭环是比例控制,第二个是积分控制,最下面一个是比例积分控制,为方便对比我们稍稍做下参数调整,将比例积分控制的 KKK
最上面一个闭环是比例控制,第二个是积分控制,最下面一个是比例积分控制,为方便对比我们稍稍做下参数调整,将比例积分控制的 KKKi 增加到 222,看看效果
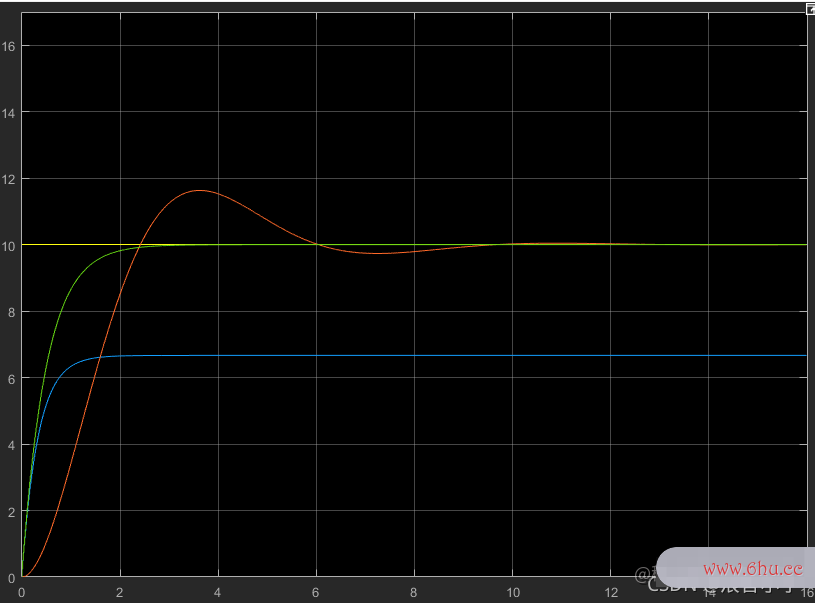 这条绿色的线就是比例积分控制,其余三条不变。由图可知,比例积分控制不仅吸取了比例控制的快速响应并稳定特点,还吸取了积分控制能消除稳态误差的特点,所以比例积分控制的有点明显胜于比例控制。
这条绿色的线就是比例积分控制,其余三条不变。由图可知,比例积分控制不仅吸取了比例控制的快速响应并稳定特点,还吸取了积分控制能消除稳态误差的特点,所以比例积分控制的有点明显胜于比例控制。
引入微分控制
设一个二阶系统的一对根为 ppp1 =−a+bi= – a + bi=−a+bi , ppp2 =−a−bi= – a – bi=−a−bi,对该系统输入一个单位冲激信号,那么该系统的响应为
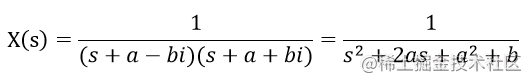 经过拉普拉斯逆变换后,得
经过拉普拉斯逆变换后,得
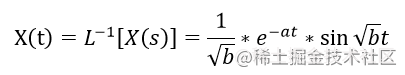 我们知道这个函数得曲线是振荡衰减直至到000,也就是说这个系统是稳定的。我们的目标是让系统更快速稳定,也就是加快系统的收敛速度,也就是−a-a−a 越小,系统的收敛的速度才会越快,减小 −a-a−a 也就是改变根轨迹,让根左移。我们以实例来说明:
设有系统的开环传递函数为
我们知道这个函数得曲线是振荡衰减直至到000,也就是说这个系统是稳定的。我们的目标是让系统更快速稳定,也就是加快系统的收敛速度,也就是−a-a−a 越小,系统的收敛的速度才会越快,减小 −a-a−a 也就是改变根轨迹,让根左移。我们以实例来说明:
设有系统的开环传递函数为
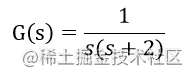 该系统有222个极点,
该系统有222个极点,1=== 000,2=== −2-2−2,没有零点,渐近线交点a=$$-1,与实轴得交角为909090,根轨迹如下
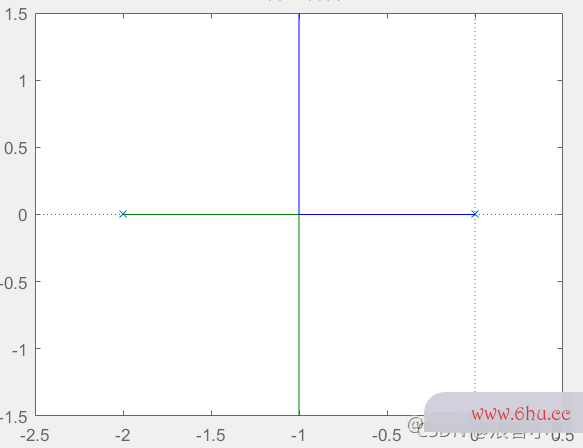 那么所有的根都将在实部为−1-1−1这条竖线上,我们要让系统快速衰减,也就是让根左移,并且越左越好,我们就让他移到实部为−2-2−2得这条竖线上,为便于计算,我们设这个根为k=−2+2√3ik=-2+2√3ik=−2+2√3i。
那么所有的根都将在实部为−1-1−1这条竖线上,我们要让系统快速衰减,也就是让根左移,并且越左越好,我们就让他移到实部为−2-2−2得这条竖线上,为便于计算,我们设这个根为k=−2+2√3ik=-2+2√3ik=−2+2√3i。
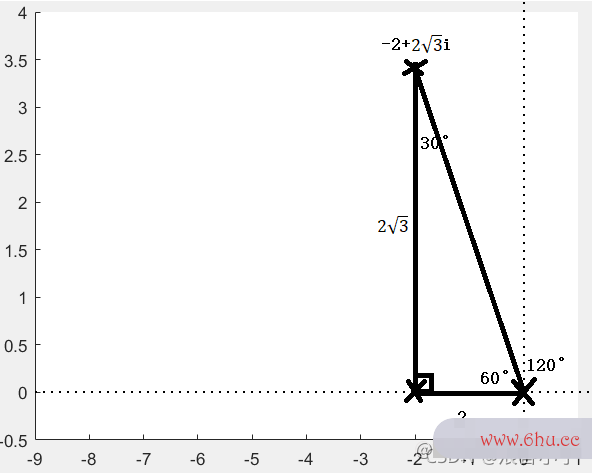 根据幅角条件
根据幅角条件
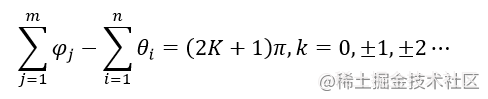 得
得
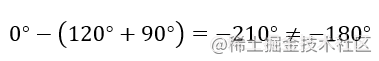 这也就是说,k=−2+2√3ik=-2+2√3ik=−2+2√3i不在原根轨迹上,如果要使这个根满足幅角条件,或者说改变原根轨迹使得kkk在新的根轨迹上,该怎么办呢?那就加个30,也就是加个零点嘛,如图
这也就是说,k=−2+2√3ik=-2+2√3ik=−2+2√3i不在原根轨迹上,如果要使这个根满足幅角条件,或者说改变原根轨迹使得kkk在新的根轨迹上,该怎么办呢?那就加个30,也就是加个零点嘛,如图
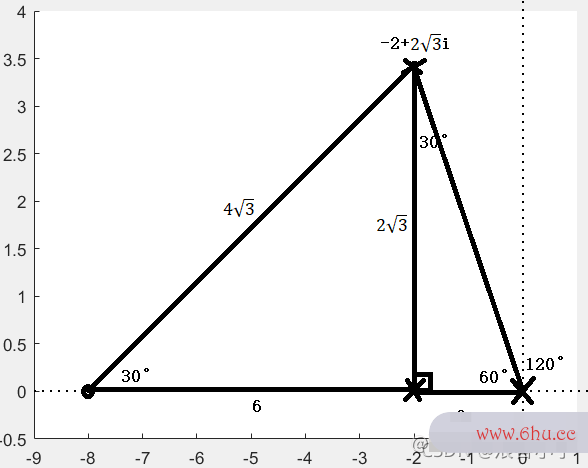 通过计算,补偿的30这个零点为−8-8−8,那么这个新的控制器不就是H(s)=s+8H(s)=s+8H(s)=s+8,这不就是微分控制和比例控制吗,即PDPDPD控制,这里就把微分控制引进来了,我们可以仿真一下
通过计算,补偿的30这个零点为−8-8−8,那么这个新的控制器不就是H(s)=s+8H(s)=s+8H(s)=s+8,这不就是微分控制和比例控制吗,即PDPDPD控制,这里就把微分控制引进来了,我们可以仿真一下
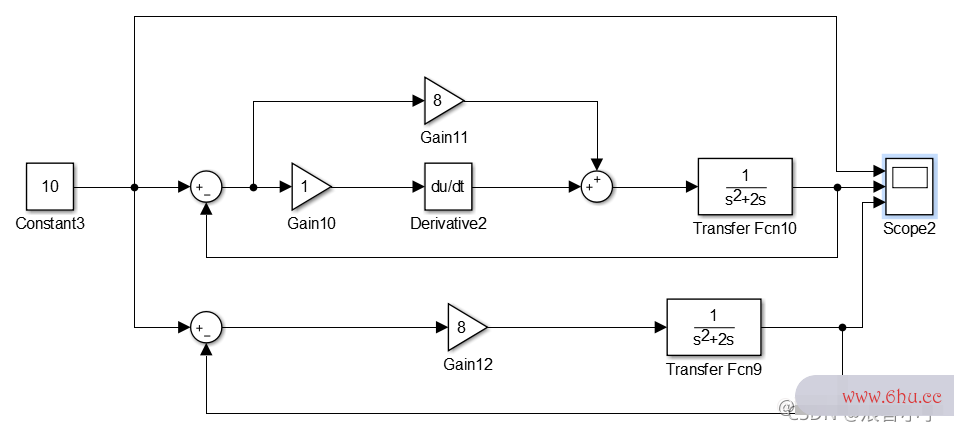 这个结构中,上面一个闭环是PDPDPD控制,下面一个就是PPP控制,KpK~p~Kp =8=8=8,得到得输出响应
这个结构中,上面一个闭环是PDPDPD控制,下面一个就是PPP控制,KpK~p~Kp =8=8=8,得到得输出响应
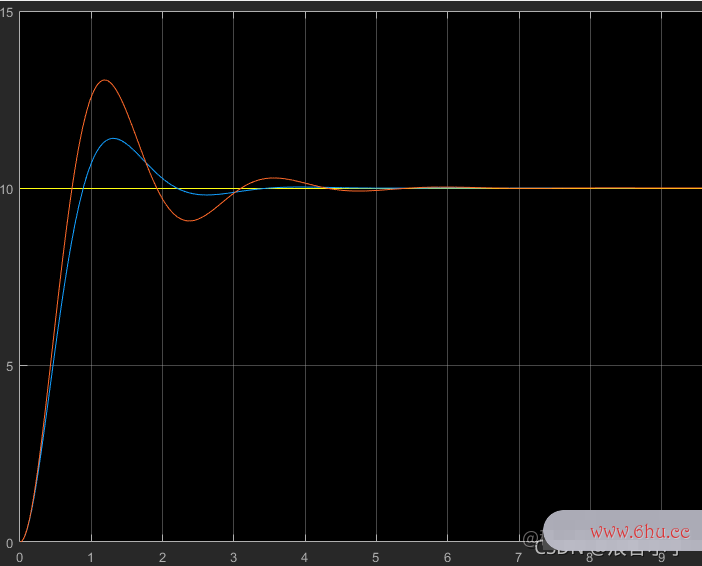 蓝色的线表示PDPDPD控制,橙黄色得线表示PPP控制,可以清楚得看到PDPDPD控制得超调要小的多,收敛的速度也明显比比例控制快很多。我们在修改修改参数,将KKK
蓝色的线表示PDPDPD控制,橙黄色得线表示PPP控制,可以清楚得看到PDPDPD控制得超调要小的多,收敛的速度也明显比比例控制快很多。我们在修改修改参数,将KKKi =2.9=2.9=2.9,看看效果
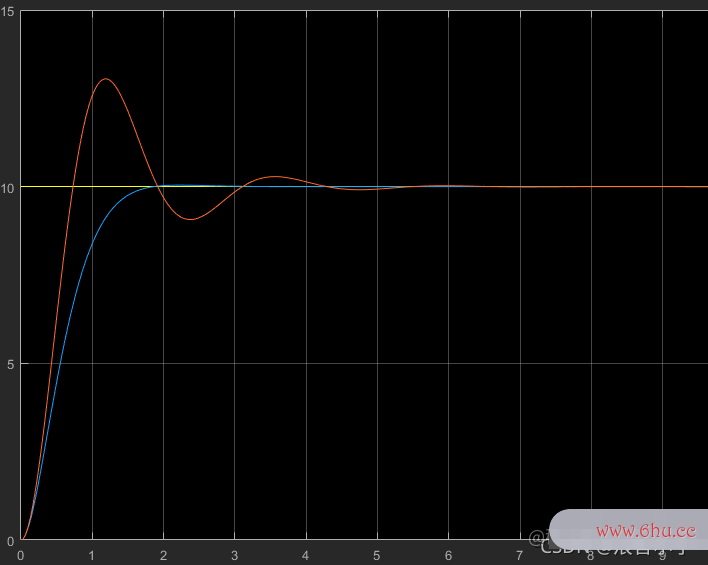 很明显,现在的超调已经变得很小了,收敛速度更快。对于微分控制,在实际应用中,不会拿微分控制单独做一个控制器,因为微分控制对高频干扰十分敏感,比如在系统中存在这样一个干扰:D(t)=0.01sin(100t)D(t)=0.01sin(100t)D(t)=0.01sin(100t),它的幅值很小,频率很高,一旦遇到微分控制,于是D(t)D(t)D(t)对ttt求导,此时 DDD^1^(t)=cos(100t)cos(100t)cos(100t),赋值被放大了100倍,所以微分控制在很多时候并不被使用,PIPIPI控制被广泛应用。
很明显,现在的超调已经变得很小了,收敛速度更快。对于微分控制,在实际应用中,不会拿微分控制单独做一个控制器,因为微分控制对高频干扰十分敏感,比如在系统中存在这样一个干扰:D(t)=0.01sin(100t)D(t)=0.01sin(100t)D(t)=0.01sin(100t),它的幅值很小,频率很高,一旦遇到微分控制,于是D(t)D(t)D(t)对ttt求导,此时 DDD^1^(t)=cos(100t)cos(100t)cos(100t),赋值被放大了100倍,所以微分控制在很多时候并不被使用,PIPIPI控制被广泛应用。


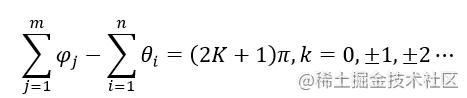
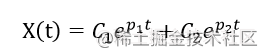
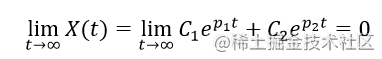

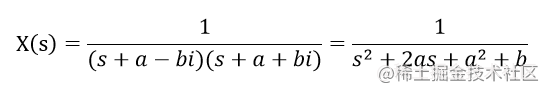
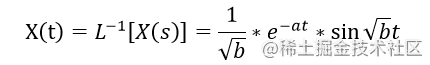

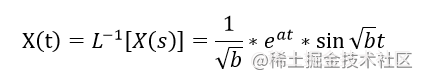

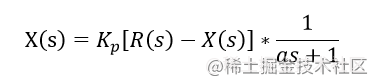
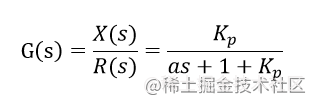
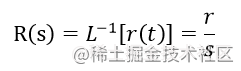

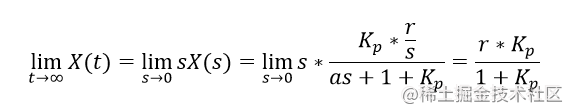
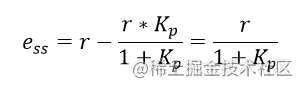






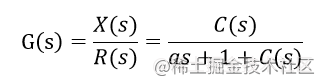
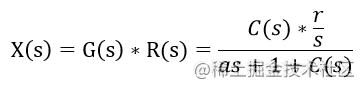
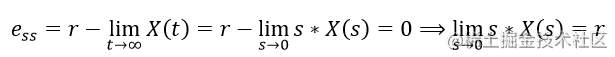
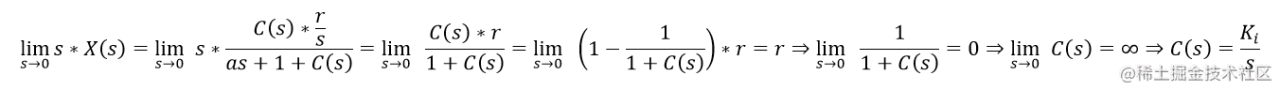




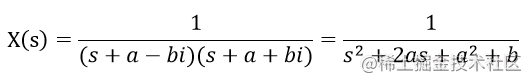
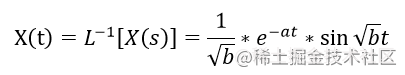
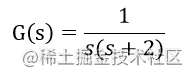


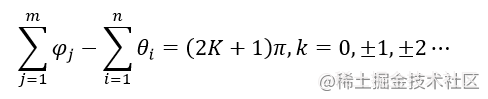
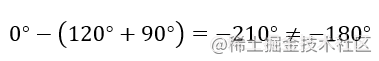





评论(0)